
【題目】已知函數![]() ,
,![]() ,其中
,其中![]() ,設
,設 .
.
(1)如果![]() 為奇函數,求實數
為奇函數,求實數![]() 、
、![]() 滿足的條件;
滿足的條件;
(2)在(1)的條件下,若函數![]() 在區間
在區間![]() 上為增函數,求
上為增函數,求![]() 的取值范圍;
的取值范圍;
(3)若對任意的![]() 恒有
恒有![]() 成立.證明:當
成立.證明:當![]() 時,
時,![]() 成立.
成立.
【答案】(1)![]() ,
,![]() ;(2)
;(2)![]() ;(3)見解析
;(3)見解析
【解析】
(1)根據函數為奇函數,利用奇函數對應的表達式,得到關于![]() 的關系式,分析等式恒成立的條件即可得到
的關系式,分析等式恒成立的條件即可得到![]() 滿足的條件;
滿足的條件;
(2)利用函數單調性的定義,求解出關于![]() 的不等式,即可求解出
的不等式,即可求解出![]() 的取值范圍;
的取值范圍;
(3)由![]() 得到
得到![]() 間的不等關系,再根據作差法以及不等式的性質證明
間的不等關系,再根據作差法以及不等式的性質證明![]() 在
在![]() 時成立.
時成立.
(1)![]() ,設
,設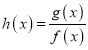 的定義域為
的定義域為![]() ,
,
∵![]() 為奇函數,∴對于任意
為奇函數,∴對于任意![]() ,
,![]() 成立.
成立.
即:![]() 化簡得:
化簡得:![]() ,
,
因對于任意![]() 都成立,
都成立,
∴![]() ,
,
即![]() ,
,![]() .
.
(2)由(1)知![]() ,
,![]() ,
,
∵![]() 在
在![]() 上為增函數,
上為增函數,
∴任取![]() 時,
時,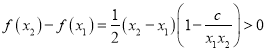 恒成立.
恒成立.
即任取![]() 時,
時,![]() 成立,
成立,
也就是![]() 成立.
成立.
∴![]() ,即
,即![]() 的取值范圍是
的取值范圍是![]() .
.
(3)因為任意的![]() 恒有
恒有![]() 成立,
成立,
所以對任意的![]() ,
,![]() ,
,
即![]() 恒成立.
恒成立.
所以判別式![]() ,
,
從而![]() ,∴
,∴![]() ,且
,且![]() ,
,
因此![]() 且
且![]() .
.
故當![]() 時,有
時,有![]() .
.
即當![]() 時,
時,![]() 成立.
成立.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:高中數學 來源: 題型:
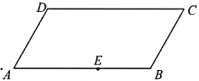
【題目】下圖是一塊平行四邊形園地![]() ,經測量,
,經測量,![]()
![]() .擬過線段
.擬過線段![]() 上一點
上一點![]() 設計一條直路
設計一條直路![]() (點
(點![]() 在四邊形
在四邊形![]() 的邊上,不計直路的寬度),將該園地分為面積之比為
的邊上,不計直路的寬度),將該園地分為面積之比為![]() 的左,右兩部分分別種植不同花卉.設
的左,右兩部分分別種植不同花卉.設![]() (單位:m).
(單位:m).
(1)當點![]() 與點
與點![]() 重合時,試確定點
重合時,試確定點![]() 的位置;
的位置;
(2)求![]() 關于
關于![]() 的函數關系式;
的函數關系式;
(3)試確定點![]() 的位置,使直路
的位置,使直路![]() 的長度最短.
的長度最短.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知集合M是具有下列性質的函數![]() 的全體:存在實數對
的全體:存在實數對![]() ,使得
,使得![]() 對定義域內任意實數x都成立.
對定義域內任意實數x都成立.
(1)判斷函數![]() ,
,![]() 是否屬于集合
是否屬于集合![]() ;
;
(2)若函數![]() 具有反函數
具有反函數![]() ,是否存在相同的實數對
,是否存在相同的實數對![]() ,使得
,使得![]() 與
與![]() 同時屬于集合
同時屬于集合![]()
![]() 若存在,求出相應的
若存在,求出相應的![]() ;若不存在,說明理由;
;若不存在,說明理由;
(3)若定義域為![]() 的函數
的函數![]() 屬于集合
屬于集合![]() ,且存在滿足有序實數對
,且存在滿足有序實數對![]() 和
和![]() ;當
;當![]() 時,
時,![]() 的值域為
的值域為![]() ,求當
,求當![]() 時函數
時函數![]() 的值域.
的值域.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】空氣質量指數PM2.5(單位:μg/m3)表示每立方米空氣中可入肺顆粒物的含量,這個值越高,就代表空氣污染越嚴重:
日均濃度 |
|
|
|
|
|
|
空氣質量級別 | 一級 | 二級 | 三級 | 四級 | 五級 | 六級 |
空氣質量類型 | 優 | 良 | 輕度污染 | 中度污染 | 重度污染 | 嚴重污染 |
甲、乙兩城市2013年2月份中的15天對空氣質量指數PM2.5進行監測,獲得PM2.5日均濃度指數數據如莖葉圖所示:
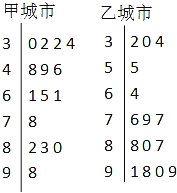
(Ⅰ)根據你所學的統計知識估計甲、乙兩城市15天內哪個城市空氣質量總體較好?(注:不需說明理由)
(Ⅱ)在15天內任取1天,估計甲、乙兩城市空氣質量類別均為優或良的概率;
(Ⅲ)在乙城市15個監測數據中任取2個,設X為空氣質量類別為優或良的天數,求X的分布列及數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】![]() 的內切圓與三邊
的內切圓與三邊![]() 的切點分別為
的切點分別為![]() ,已知
,已知![]() ,內切圓圓心
,內切圓圓心![]() ,設點A的軌跡為R.
,設點A的軌跡為R.
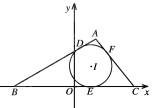
(1)求R的方程;
(2)過點C的動直線m交曲線R于不同的兩點M,N,問在x軸上是否存在一定點Q(Q不與C重合),使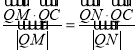 恒成立,若求出Q點的坐標,若不存在,說明理由.
恒成立,若求出Q點的坐標,若不存在,說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】若函數![]() 對其定義域內的任意
對其定義域內的任意![]() ,
,![]() ,當
,當![]() 時總有
時總有![]() ,則稱
,則稱![]() 為緊密函數,例如函數
為緊密函數,例如函數![]() 是緊密函數,下列命題:
是緊密函數,下列命題:
![]() 緊密函數必是單調函數;
緊密函數必是單調函數;![]() 函數
函數![]() 在
在![]() 時是緊密函數;
時是緊密函數;
![]() 函數
函數![]() 是緊密函數;
是緊密函數;
![]() 若函數
若函數![]() 為定義域內的緊密函數,
為定義域內的緊密函數,![]() ,則
,則![]() ;
;
![]() 若函數
若函數![]() 是緊密函數且在定義域內存在導數,則其導函數
是緊密函數且在定義域內存在導數,則其導函數![]() 在定義域內的值一定不為零.
在定義域內的值一定不為零.
其中的真命題是______.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】中醫藥,是包括漢族和少數民族醫藥在內的我國各民族醫藥的統稱,是反映中華民族對生命、健康和疾病的認識,具有悠久歷史傳統和獨特理論及技術方法的醫藥學體系,是中華民族的瑰寶.某科研機構研究發現,某品種中醫藥的藥物成分甲的含量![]() (單位:克)與藥物功效
(單位:克)與藥物功效![]() (單位:藥物單位)之間具有關系
(單位:藥物單位)之間具有關系![]() .檢測這種藥品一個批次的5個樣本,得到成分甲的平均值為4克,標準差為
.檢測這種藥品一個批次的5個樣本,得到成分甲的平均值為4克,標準差為![]() 克,則估計這批中醫藥的藥物功效的平均值為( )
克,則估計這批中醫藥的藥物功效的平均值為( )
A.22藥物單位B.20藥物單位C.12藥物單位D.10藥物單位
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com