
【題目】已知函數![]() ,其中
,其中![]() 為常數.
為常數.
(1)討論函數![]() 的單調性;
的單調性;
(2)若![]() 存在兩個極值點
存在兩個極值點![]() ,求證:無論實數
,求證:無論實數![]() 取什么值都有
取什么值都有![]() .
.
【答案】(1)答案見解析; (2)證明過程見解析.
【解析】
試題分析:(1)先求得定義域為![]() ,求導通分后研究導函數的分子,利用判別式對分子根的個數和分布進行分類討論,由此求得函數的單調區間;(2)由(1)知
,求導通分后研究導函數的分子,利用判別式對分子根的個數和分布進行分類討論,由此求得函數的單調區間;(2)由(1)知![]() 時有兩個極值點,且
時有兩個極值點,且![]() ,由此利用差比較法,計算
,由此利用差比較法,計算![]() 的最小值為
的最小值為![]() ,即可得證.
,即可得證.
試題解析:(1)函數的定義域為![]() .
.
![]() ,記
,記![]() ,判別式
,判別式![]() .
.
①當![]() 即
即![]() 時,
時,![]() 恒成立,
恒成立,![]() ,所以
,所以![]() 在區間
在區間![]() 上單調遞增.
上單調遞增.
②當![]() 或
或![]() 時,方程
時,方程![]() 有兩個不同的實數根
有兩個不同的實數根![]() ,記
,記![]() ,
,![]() ,顯然
,顯然![]()
(ⅰ)若![]() ,
,![]() 圖象的對稱軸
圖象的對稱軸![]() ,
,![]() .
.
兩根![]() 在區間
在區間![]() 上,可知當
上,可知當![]() 時函數
時函數![]() 單調遞增,
單調遞增,![]() ,所以
,所以![]() ,所以
,所以![]() 在區間
在區間![]() 上遞增.
上遞增.
(ⅱ)若![]() ,則
,則![]() 圖象的對稱軸
圖象的對稱軸![]() ,
,![]() .,所以
.,所以![]() ,當
,當![]() 時,
時,![]() ,所以
,所以![]() ,所以
,所以![]() 在
在![]() 上單調遞減.當
上單調遞減.當![]() 或
或![]() 時,
時,![]() ,所以
,所以![]() ,所以
,所以![]() 在
在![]() 上單調遞增.
上單調遞增.
綜上,當![]() 時,
時,![]() 在區間
在區間![]() 上單調遞增;當
上單調遞增;當![]() 時,
時,![]() 在
在![]() 上單調遞減,在
上單調遞減,在![]() 上單調遞增.
上單調遞增.
(2)由(1)知當![]() 時,
時,![]() 沒有極值點,當
沒有極值點,當![]() 時,
時,![]() 有兩個極值點
有兩個極值點![]() ,且
,且![]() .
.
![]() ,
,
∴![]() 又
又![]() ,
,
![]() .記
.記![]() ,
,![]() ,則
,則![]() ,所以
,所以![]() 在
在![]() 時單調遞增,
時單調遞增,![]() ,所以
,所以![]() ,所以
,所以![]() .
.


科目:高中數學 來源: 題型:
【題目】據悉遵義市紅花崗區、匯川區2017年現有人口總數為110萬人,如果年自然增長率為![]() %,試解答以下問題:
%,試解答以下問題:
(1)寫出經過![]() 年后,遵義市人口總數
年后,遵義市人口總數![]() (單位:萬人)關于
(單位:萬人)關于![]() 的函數關系式;
的函數關系式;
(2)計算10年以后遵義市人口總數(精確到0.1萬人);
(3)計算經過多少年后遵義市人口將達到150萬人(精確到1年)
(參考數據: ![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設函數![]() 的定義域為D,若函數
的定義域為D,若函數![]() 滿足條件:存在
滿足條件:存在![]() ,使
,使![]() 在
在![]() 上的值域為
上的值域為![]() ,則稱
,則稱![]() 為“倍縮函數”,若函數
為“倍縮函數”,若函數![]() 為“倍縮函數”,則實數
為“倍縮函數”,則實數![]() 的取值范圍是( )
的取值范圍是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() :
:![]() 的左焦點為
的左焦點為![]() ,其左、右頂點為
,其左、右頂點為![]() 、
、![]() ,橢圓與
,橢圓與![]() 軸正半軸的交點為
軸正半軸的交點為![]() ,
,![]() 的外接圓的圓心
的外接圓的圓心![]() 在直線
在直線![]() 上.
上.
(I)求橢圓![]() 的方程;
的方程;
(II)已知直線![]() :
:![]() ,
,![]() 是橢圓
是橢圓![]() 上的動點,
上的動點,![]() ,垂足為
,垂足為![]() ,是否存在點
,是否存在點![]() ,使得
,使得![]() 為等腰三角形?若存在,求出點
為等腰三角形?若存在,求出點![]() 的坐標,若不存在,請說明理由.
的坐標,若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知拋物線![]() ,圓
,圓![]() ,點
,點![]() 為拋物線
為拋物線![]() 上的動點,
上的動點,![]() 為坐標原點,線段
為坐標原點,線段![]() 的中點
的中點![]() 的軌跡為曲線
的軌跡為曲線![]() .
.
(1)求拋物線![]() 的方程;
的方程;
(2)點![]() 是曲線
是曲線![]() 上的點,過點
上的點,過點![]() 作圓
作圓![]() 的兩條切線,分別與
的兩條切線,分別與![]() 軸交于
軸交于![]() 兩點.
兩點.
求![]() 面積的最小值.
面積的最小值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為了增強環保意識,某社團從男生中隨機抽取了60人,從女生中隨機抽取了50人參加環保知識測試,統計數據如下表所示:
優秀 | 非優秀 | 總計 | |
男生 | 40 | 20 | 60 |
女生 | 20 | 30 | 50 |
總計 | 60 | 50 | 110 |
(1)試判斷是否有99%的把握認為環保知識是否優秀與性別有關;
(2)為參加市舉辦的環保知識競賽,學校舉辦預選賽,現在環保測試優秀的同學中選3人參加預選賽,已知在環保測試中優秀的同學通過預選賽的概率為![]() ,若隨機變量
,若隨機變量![]() 表示這3人中通過預選賽的人數,求
表示這3人中通過預選賽的人數,求![]() 的分布列與數學期望.
的分布列與數學期望.
附:![]() =
=![]()
| 0.500 | 0.400 | 0.100 | 0.010 | 0.001 |
| 0.455 | 0.708 | 2.706 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為減少空氣污染,某市鼓勵居民用電(減少燃氣或燃煤),采用分段計費的方法計算:電費每月用電不超過100度時,按每度0.57元計算;每月用電量超過100度時,其中的100度仍按原標準收費,超過的部分每度按0.5元計算.
(Ⅰ)設月用電![]() 度時,應交電費
度時,應交電費![]() 元,寫出
元,寫出![]() 關于
關于![]() 的函數關系式;
的函數關系式;
(Ⅱ)小明家第一季度繳納電費情況如下:
月份 | 一月 | 二月 | 三月 | 合計 |
交費金額 | 76元 | 63元 | 45.6元 | 184.6元 |
問小明家第一季度共用電多少度?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某種產品的廣告費用支出![]() 與銷售額
與銷售額![]() 之間有如下的對應數據:
之間有如下的對應數據:
| 2 | 4 | 5 | 6 | 8 |
| 30 | 40 | 60 | 50 | 70 |
(1)畫出散點圖;并說明銷售額y與廣告費用支出x之間是正相關還是負相關?
(2)請根據上表提供的數據,求回歸直線方程![]() ;
;
(3)據此估計廣告費用為10時,銷售收入![]() 的值.
的值.
(參考公式: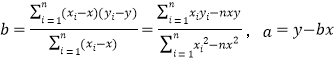 ,).
,).
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() .
.
(1)當![]() 時,求函數
時,求函數![]() 在
在![]() 上的最大值;
上的最大值;
(2)令![]() ,若
,若![]() 在區間
在區間![]() 上為單調遞增函數,求
上為單調遞增函數,求![]() 的取值范圍;
的取值范圍;
(3)當![]() 時,函數
時,函數![]() 的圖象與
的圖象與![]() 軸交于兩點
軸交于兩點![]() ,且
,且![]() ,又
,又![]() 是
是![]() 的導函數.若正常數
的導函數.若正常數![]() 滿足條件
滿足條件![]() .試比較
.試比較![]() 與0的關系,并給出理由.
與0的關系,并給出理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com