
【題目】如圖,四棱錐![]() 中,
中, ![]() 為等邊三角形,且平面
為等邊三角形,且平面![]() 平面
平面![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
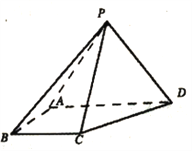
(Ⅰ)證明: ![]() ;
;
(Ⅱ)若直線![]() 與平面
與平面![]() 所成角為
所成角為![]() ,求二面角
,求二面角![]() 的余弦值.
的余弦值.
【答案】證明見解析;(Ⅱ) ![]() .
.
【解析】試題分析:
(Ⅰ)取![]() 的中點為
的中點為![]() ,連接
,連接![]() ,
, ![]() ,結合條件可證得
,結合條件可證得![]() 平面
平面![]() ,于是
,于是![]() ,又
,又![]() ,故可得
,故可得![]() .(Ⅱ)由題意可證得
.(Ⅱ)由題意可證得![]() ,
, ![]() ,
, ![]() 兩兩垂直,建立空間直角坐標系,通過求出平面
兩兩垂直,建立空間直角坐標系,通過求出平面![]() 和平面
和平面![]() 的法向量可求解本題.
的法向量可求解本題.
試題解析:
證明:(Ⅰ)取![]() 的中點為
的中點為![]() ,連接
,連接![]() ,
, ![]() ,
,
∵![]() 為等邊三角形,
為等邊三角形,
∴![]() .
.
在底面![]() 中,可得四邊形
中,可得四邊形![]() 為矩形,
為矩形,
∴![]() ,
,
∵![]() ,
,
∴![]() 平面
平面![]() ,
,
∵![]() 平面
平面![]() ,
,
∴![]() .
.
又![]() ,
,
∴![]() .
.
(Ⅱ)∵平面![]() 面
面![]() ,
, ![]() ,
,
∴![]() 平面
平面![]() ,
,
由此可得![]() ,
, ![]() ,
, ![]() 兩兩垂直,建立如圖所示的空間直角坐標系
兩兩垂直,建立如圖所示的空間直角坐標系![]() .
.
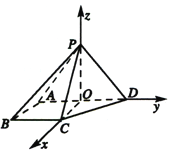
∵直線![]() 與平面
與平面![]() 所成角為
所成角為![]() ,即
,即![]() ,
,
由![]() ,知
,知![]() ,得
,得![]() .
.
則![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,
![]() ,
, ![]() ,
, ![]() ,
,
設平面![]() 的一個法向量為
的一個法向量為![]() .
.
由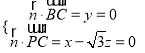 ,得
,得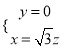 .
.
令![]() ,則
,則![]() .
.
設平面![]() 的一個法向量為
的一個法向量為![]() ,
,
由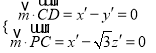 ,得
,得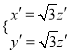 .
.
令![]() ,則
,則![]() ,
,
∴![]()
![]()
![]() ,
,
由圖形知二面角![]() 為鈍角,
為鈍角,
∴二面角![]() 的余弦值為
的余弦值為![]() .
.


科目:高中數學 來源: 題型:
【題目】設函數f (x)=ln x-x+1.
(1)討論函數f (x)的單調性;
(2)證明當x∈(1,+∞)時, ![]() ;
;
(3)設c>1,證明當x∈(0,1)時,1+(c-1)x>cx.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在某親子游戲結束時有一項抽獎活動,抽獎規則是:盒子里面共有5個小球,小球上分別寫有0,1,2,3,4的數字,小球除數字外其它完全相同,每對親子中,家長先從盒子中取出一個小球,記下數字后將小球放回,孩子再從盒子中取出一個小球,記下小球上數字將小球放回.抽獎活動的獎勵規則是:①若取出的兩個小球上數字之積大于8,則獎勵飛機玩具一個;②若取出的兩個小球上數字之積在區間![]() 上,則獎勵汽車玩具一個;③若取出的兩個小球上數字之積小于2,則獎勵飲料一瓶.
上,則獎勵汽車玩具一個;③若取出的兩個小球上數字之積小于2,則獎勵飲料一瓶.
(1)求每對親子獲得飛機玩具的概率;
(2)試比較每對親子獲得汽車玩具與獲得飲料的概率,哪個更大?請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某公司試銷一種成本單價為500元的新產品,規定試銷時銷售單價不低于成本單價,又不高于800元.經試銷調查,發現銷售量y(件)與銷售單價x(元)之間的關系可近似看作一次函數y=kx+b(k≠0),函數圖象如圖所示.

(1)根據圖象,求一次函數y=kx+b(k≠0)的表達式;
(2)設公司獲得的毛利潤(毛利潤=銷售總價-成本總價)為S元.試問銷售單價定為多少時,該公司可獲得最大毛利潤?最大毛利潤是多少?此時的銷售量是多少?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() :
:![]() 的離心率為
的離心率為![]() ,其左焦點與拋物線
,其左焦點與拋物線![]() 的焦點重合.
的焦點重合.
(1)求橢圓![]() 的方程;
的方程;
(2)過動點![]() 的直線交
的直線交![]() 軸于點
軸于點![]() ,交橢圓
,交橢圓![]() 于點
于點![]() ,
,![]() 在第一象限,
在第一象限,![]() ,過點
,過點![]() 做
做![]() 軸的垂線交橢圓
軸的垂線交橢圓![]() 于點
于點![]() ,連接
,連接![]() 并延長交橢圓
并延長交橢圓![]() 于另一點
于另一點![]() .設直線
.設直線![]() 的斜率分別為
的斜率分別為![]() ,證明:
,證明:![]() 為定值.
為定值.

查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在四棱錐PABCD中,AB∥CD ,且∠BAP=∠CDP =90°.
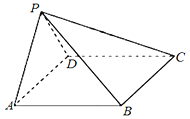
(1).證明:平面PAB⊥平面PAD;
(2).若PA=PD=AB=DC, ∠APD =90°,且四棱錐PABCD的體積為![]() ,求該四棱錐的側面積.
,求該四棱錐的側面積.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com