【題目】已知函數
．
（1）求函數
的最小正周期、最小值、對稱軸、對稱中心；
（2）設
的內角
的對邊分別為
，且
，若
，求
的值．
【答案】(1) 最小正周期是
，最小值是-2. 對稱軸為
；對稱中心為
；(2) 
.
【解析】
(1)先根據兩角和與差的正弦公式化簡為
的形式,結合正弦函數的最值,對稱軸和對稱中心可得到函數
的最小值,對稱軸和對稱中心,再由
可求出其最小正周期.
(2)由(1)確定的的解析式及
,求出
.由
的范圍,求出
的范圍,利用特殊角的三角函數值及正弦函數的圖象求出角的度數,由
,利用正弦定理得到
,再利用余弦定理得到
,將
與
的值代入得到關于
和
的方程求出與的值.
解：（1）∵
=
,
∴的最小正周期是
，最小值是-2.
令
，則的對稱軸為,
令
，則的對稱中心為,
（2）
,則
=1,
,
,
,解得
,
又
，由正弦定理得
①,
由余弦定理得
，即3=
②,
由①②解得.
閱讀快車系列答案科目：高中數學 來源： 題型：
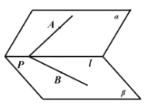
【題目】如圖，二面角
中，
，射線
，
分別在平面
，
內，點A在平面內的射影恰好是點B，設二面角、與平面所成角、與平面所成角的大小分別為
，則（ ）
A.
B.
C.
D.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知函數
．
（Ⅰ）若關于
的不等式
在
上恒成立，求
的取值范圍；
（Ⅱ）設函數
，在（Ⅰ）的條件下，試判斷
在
上是否存在極值．若存在，判斷極值的正負；若不存在，請說明理由．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某冰糖橙，甜橙的一種，云南著名特產，以味甜皮薄著稱。該橙按照等級可分為四類：珍品、特級、優級和一級（每箱有5kg）,某采購商打算訂購一批橙子銷往省外，并從采購的這批橙子中隨機抽取100箱，利用橙子的等級分類標準得到的數據如下表：
等級 | 珍品 | 特級 | 優級 | 一級 |
箱數 | 40 | 30 | 10 | 20 |
（1）若將頻率改為概率，從這100箱橙子中有放回地隨機抽取4箱，求恰好抽到2箱是一級品的概率：
（2）利用樣本估計總體，莊園老板提出兩種購銷方案供采購商參考：
方案一：不分等級賣出，價格為27元/kg;
方案二：分等級賣出，分等級的橙子價格如下：
等級 | 珍品 | 特級 | 優級 | 一級 |
售價（元/kg） | 36 | 30 | 24 | 18 |
從采購商的角度考慮，應該采用哪種方案？
（3）用分層抽樣的方法從這100箱橙子中抽取10箱，再從抽取的10箱中隨機抽取3箱，X表示抽取的是珍品等級，求x的分布列及數學期望E（X）.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】“大眾創業，萬眾創新”是李克強總理在本屆政府工作報告中向全國人民發出的口號．某生產企業積極響應號召，大力研發新產品，為了對新研發的一批產品進行合理定價，將該產品按事先擬定的價格進行試銷，得到一組銷售數據
（
=1,2，…，6），如表所示：
試銷單價 | 4 | 5 | 6 | 7 | 8 | 9 |
產品銷量 | q | 84 | 83 | 80 | 75 | 68 |
已知
．
（Ⅰ）求出
的值；
（Ⅱ）已知變量
具有線性相關關系，求產品銷量
（件）關于試銷單價
（元）的線性回歸方程
；
（參考公式：線性回歸方程中
，
的最小二乘估計分別為
,
)
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖，在四棱錐
中，
，
，
，且
，
.
（1）證明：
面
；
（2）在
上是否存在點
，使
平面
，若存在，請計算
的值，若不存在，請說明理由；
（3）若
，求點
到平面的距離.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】設函數
.
（1）求f（x）的單調區間；
（2）若當
時，不等式f （x）＜m恒成立，求實數m的取值范圍；
（3）若關于x的方程f（x）＝x2+x+a在區間[0，2]上恰好有兩個相異的實根，求實數a的取值范圍．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】甲、乙兩品牌計劃入駐某商場，該商場批準兩個品牌先進場試銷
天。兩品牌提供的返利方案如下：甲品牌無固定返利，賣出
件以內（含件）的產品，每件產品返利元，超出件的部分每件返利
元；乙品牌每天固定返利
元，且每賣出一件產品再返利
元。經統計，兩家品牌在試銷期間的銷售件數的莖葉圖如下：
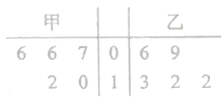
（Ⅰ）現從乙品牌試銷的天中隨機抽取天，求這天的銷售量中至少有一天低于的概率.
（Ⅱ）若將頻率視作概率，回答以下問題：
①記甲品牌的日返利額為
（單位：元），求的分布列和數學期望；
②商場擬在甲、乙兩品牌中選擇一個長期銷售，如果僅從日返利額的角度考慮，請利用所學的統計學知識為商場作出選擇，并說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
