
【題目】已知函數 ![]() ,
,
(1)求f(x)的定義域;
(2)求使f(x)>0的x的取值范圍.
【答案】
(1)解:求函數 ![]() 的定義域,
的定義域,
即: ![]() .
.
所以,定義域是(﹣1,1)
(2)解: ![]()
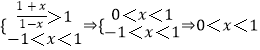
所以x的取值范圍為0<x<1
【解析】首先對于(1)分析對數函數 ![]() ,所以定義域應為
,所以定義域應為 ![]() ,解出即可得到答案.對于(2)f(x)>0,列出式子
,解出即可得到答案.對于(2)f(x)>0,列出式子 ![]() ,且要滿足x屬于定義域,解不等式即可.
,且要滿足x屬于定義域,解不等式即可.
【考點精析】通過靈活運用函數單調性的判斷方法和對數函數的單調性與特殊點,掌握單調性的判定法:①設x1,x2是所研究區間內任兩個自變量,且x1<x2;②判定f(x1)與f(x2)的大小;③作差比較或作商比較;過定點(1,0),即x=1時,y=0;a>1時在(0,+∞)上是增函數;0>a>1時在(0,+∞)上是減函數即可以解答此題.


 課堂練加測系列答案
課堂練加測系列答案 輕松課堂單元測試AB卷系列答案
輕松課堂單元測試AB卷系列答案科目:高中數學 來源: 題型:
【題目】如圖,四棱錐P﹣ABCD的底面ABCD是矩形,平面PAB⊥平面ABCD,PA=AB=3,BC=2,E、F分別是棱AD,PC的中點 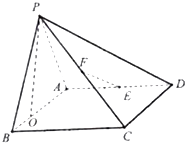
(1)求證:EF⊥平面PBC
(2)若直線PC與平面ABCD所成角為 ![]() ,點P在AB上的射影O在靠近點B的一側,求二面角P﹣EF﹣A的余弦值.
,點P在AB上的射影O在靠近點B的一側,求二面角P﹣EF﹣A的余弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設f(x)=(log2x)2﹣2alog2x+b(x>0).當x= ![]() 時,f(x)有最小值﹣1.
時,f(x)有最小值﹣1.
(1)求a與b的值;
(2)求滿足f(x)<0的x的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知圓![]() ,
, ![]() 在拋物線
在拋物線![]() 上,圓
上,圓![]() 過原點且與
過原點且與![]() 的準線相切.
的準線相切.
(Ⅰ) 求![]() 的方程;
的方程;
(Ⅱ) 點![]() ,點
,點![]() (與
(與![]() 不重合)在直線
不重合)在直線![]() 上運動,過點
上運動,過點![]() 作
作![]() 的兩條切線,切點分別為
的兩條切線,切點分別為![]() ,
, ![]() .求證:
.求證: ![]() (其中
(其中![]() 為坐標原點).
為坐標原點).
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知二次函數f(x)=x2+bx+c,且f(﹣3)=f(1),f(0)=0.
(1)求函數f(x)的解析式;
(2)若函數g(x)=f(x)﹣(4+2a)x+2,x∈[1,2],求函數g(x)的最值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】《張邱建算經》是中國古代數學史上的杰作,該書中有首古民謠記載了一數列問題:“南山一棵竹, 竹尾風割斷, 剩下三十節,一節一個圈. 頭節高五寸①,頭圈一尺三②.逐節多三分③,逐圈少分三④. 一蟻往上爬,遇圈則繞圈. 爬到竹子頂,行程是多遠?”(注釋:①第一節的高度為![]() 尺;②第一圈的周長為
尺;②第一圈的周長為![]() 尺;③每節比其下面的一節多
尺;③每節比其下面的一節多![]() 尺;④每圈周長比其下面的一圈少
尺;④每圈周長比其下面的一圈少![]() 尺) 問:此民謠提出的問題的答案是
尺) 問:此民謠提出的問題的答案是
A. ![]() 尺 B.
尺 B. ![]() 尺
尺
C. ![]() 尺 D.
尺 D. ![]() 尺
尺
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設函數f(x)=x2﹣4x+3,若f(x)≥mx對任意的實數x≥2都成立,則實數m的取值范圍是( )
A.[﹣2 ![]() ﹣4,﹣2
﹣4,﹣2 ![]() ?+4]
?+4]
B.(﹣∞,﹣2 ![]() ﹣4]∪[﹣2
﹣4]∪[﹣2 ![]() ?+4,+∞)
?+4,+∞)
C.[﹣2 ![]() ?+4,+∞)
?+4,+∞)
D.(﹣∞,﹣ ![]() ]
]
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如下圖,在長方體ABCD﹣A1B1C1D1中,AD=AA1=1,AB=2,點E在棱AB上移動,則直線D1E與A1D所成角的大小是 , 若D1E⊥EC,則直線A1D與平面D1DE所成的角為 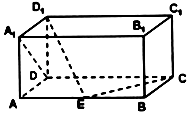
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com