
【題目】如圖1,![]() ,過動點
,過動點![]() 作
作![]() ,垂足
,垂足![]() 在線段
在線段![]() 上且異于點
上且異于點![]() ,連接
,連接![]() ,沿
,沿![]() 將
將![]() 折起,使
折起,使![]() (如圖2所示),
(如圖2所示),
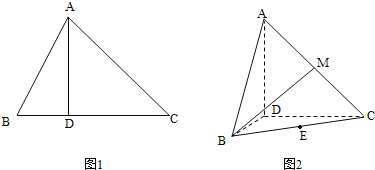
(1)當![]() 的長為多少時,三棱錐
的長為多少時,三棱錐![]() 的體積最大;
的體積最大;
(2)當三棱錐![]() 的體積最大時,設點
的體積最大時,設點![]() 分別為棱
分別為棱![]() 的中點,試在棱
的中點,試在棱![]() 上確定一點
上確定一點![]() ,使得
,使得![]() ,并求
,并求![]() 與平面
與平面![]() 所成角的大小.
所成角的大小.
【答案】(1)![]() ;(2)
;(2)![]() ,
,![]()
【解析】
(1)設![]() ,先利用線面垂直的判定定理證明
,先利用線面垂直的判定定理證明![]() 即為三棱錐
即為三棱錐![]() 的高,再將三棱錐的體積表示為
的高,再將三棱錐的體積表示為![]() 的函數,最后利用導數求函數的最大值即可;
的函數,最后利用導數求函數的最大值即可;
(2)由(1)可先建立空間直角坐標系,寫出相關點的坐標和相關向量的坐標,設出動點![]() 的坐標,先利用線線垂直的充要條件計算出
的坐標,先利用線線垂直的充要條件計算出![]() 點坐標,從而確定
點坐標,從而確定![]() 點位置,再求平面
點位置,再求平面![]() 的法向量,從而利用夾角公式即可求得所求線面角
的法向量,從而利用夾角公式即可求得所求線面角
(1)設![]() ,則
,則![]()
![]()
∵折起前![]() ,∴折起后
,∴折起后![]()
∴![]() 平面
平面![]()
∴![]()
![]()
設![]() ,
,
∵![]() ,∴
,∴![]() 在
在![]() 上為增函數,在
上為增函數,在![]() 上為減函數
上為減函數
∴當![]() 時,函數
時,函數![]() 取最大值
取最大值
∴當![]() 時,三棱錐
時,三棱錐![]() 的體積最大;
的體積最大;
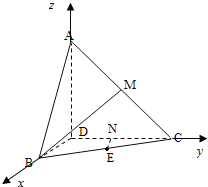
(2)以![]() 為原點,建立如圖直角坐標系
為原點,建立如圖直角坐標系![]() ,
,
由(1)知,三棱錐![]() 的體積最大時,
的體積最大時,![]() ,
,
∴![]()
![]() ,且
,且![]()
設![]() ,則
,則![]()
![]()
∵![]() ,∴
,∴![]()
即![]() ,
,
∴![]() ,∴
,∴![]() ,
,
∴當![]() 時,
時,![]()
設平面![]() 的一個法向量為
的一個法向量為![]() ,由
,由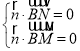 及
及![]()
得![]() ,取
,取![]()
設![]() 與平面
與平面![]() 所成角為
所成角為![]() ,則
,則![]()
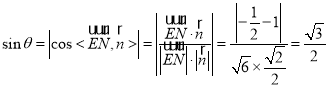 ,
,
∴![]()
∴![]() 與平面
與平面![]() 所成角的大小為
所成角的大小為![]() .
.


 學而優暑期銜接南京大學出版社系列答案
學而優暑期銜接南京大學出版社系列答案 Happy holiday歡樂假期暑假作業廣東人民出版社系列答案
Happy holiday歡樂假期暑假作業廣東人民出版社系列答案科目:高中數學 來源: 題型:
【題目】已知函數f(x)=x2﹣2acoskπlnx(k∈N*,a∈R且a>0).
(1)討論函數f(x)的單調性;
(2)若k=2018,關于x的方程f(x)=2ax有唯一解,求a的值;
(3)當k=2019時,證明:對一切x∈(0,+∞),都有![]() 成立.
成立.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】普通高中國家助學金,用于資助家庭困難的在校高中生.在本地,助學金分一等和二等兩類,一等助學金每學期1250元,二等助學金每學期750元,并規定:屬于農村建檔立卡戶的學生評一等助學金.某班有10名獲得助學金的貧困學生,其中有3名屬于農村建檔立卡戶,這10名學生中有4名獲一等助學金,另6名獲二等助學金.現從這10名學生中任選3名參加座談會.
(Ⅰ)若事件A表示“選出的3名同學既有建檔立卡戶學生,又有非建檔立卡戶學生”,求A的概率;
(Ⅱ)設X為選出的3名同學一學期獲助學金的總金額,求隨機變量X的分布列和數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]()
![]() 的上頂點為
的上頂點為![]() ,以
,以![]() 為圓心橢圓的長半軸為半徑的圓與
為圓心橢圓的長半軸為半徑的圓與![]() 軸的交點分別為
軸的交點分別為![]() ,
,![]() .
.
(1)求橢圓![]() 的標準方程;
的標準方程;
(2)設不經過點![]() 的直線
的直線![]() 與橢圓
與橢圓![]() 交于
交于![]() ,
,![]() 兩點,且
兩點,且![]() ,試探究直線
,試探究直線![]() 是否過定點?若過定點,求出該定點的坐標,若不過定點,請說明理由.
是否過定點?若過定點,求出該定點的坐標,若不過定點,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
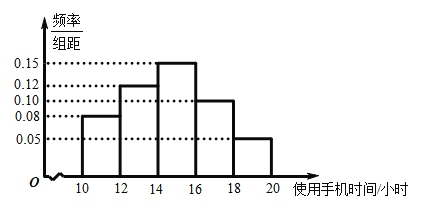
【題目】為了解學生課外使用手機的情況,某研究學習小組為研究學校學生一個月使用手機的總時間,收集了500名學生2019年12月課余使用手機的總時間(單位:小時)的數據.從中隨機抽取了50名學生,將數據進行整理,得到如圖所示的頻率分布直方圖.已知這50人中,恰有2名女生的課余使用手機總時間在![]() 區間,現在從課余使用手總時間在
區間,現在從課余使用手總時間在![]() 樣本對應的學生中隨機抽取2人,則至少抽到1名女生的概率為( )
樣本對應的學生中隨機抽取2人,則至少抽到1名女生的概率為( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
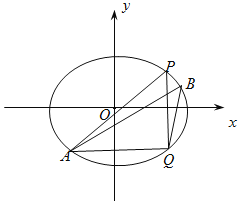
【題目】已知P(3,![]() )是橢圓C:
)是橢圓C:![]() 1
1![]() 上的點,Q是P關于x軸的對稱點,橢圓C的離心率為
上的點,Q是P關于x軸的對稱點,橢圓C的離心率為![]() .
.
(1)求橢圓C的方程;
(2)A,B是橢圓上位于直線PQ兩側的動點.
①若直線AB的斜率為![]() ,求四邊形APBQ面積的最大值.
,求四邊形APBQ面積的最大值.
②當A、B在運動過程中滿足∠APQ=∠BPQ時,問直線AB的斜率是否為定值,并說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com