Question

【題目】已知直線： ， ： ，動點分別在直線， 上移動， ， 是線段的中點.

（1）求點的軌跡的方程；

（2）設不經過坐標原點且斜率為的直線交軌跡于點，點滿足，若點在軌跡上，求四邊形的面積.

Answer 1

【答案】（I）. （II）見解析.

【解析】試題分析：（1）根據條件設， ， ，即. 設，由中點坐標公式消去參數m,n得 .

（2）設直線的方程為， ， ， .將代入，整理得 .則 ， . 因為，可得R(， . 由在橢圓上，有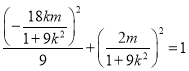，化簡得. 從而整理可得 . 可求得四邊形的面積.

試題解析：（1）根據條件可設， ，由，得:

.

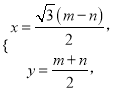設，則得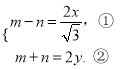

將①和②代入中并化簡得： .

所以點的軌跡的方程為.

（2）設直線的方程為， ， ， .

將代入，整理得 .

則 ， .

.

因為，則有： ， .

因為在橢圓上， ，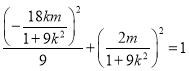

化簡得： .

所以， ，

因為

.

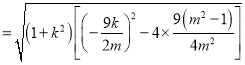
又點到的距離為.

由，可知四邊形為平行四邊形，

.

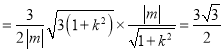拓展: 此題結論可推廣到更一般情形:

第(Ⅰ))題中, 直線、只要不垂直,軌跡均為橢圓, 、垂直時,軌跡為圓;

第(Ⅱ)題中結論可推廣到更一般情形:

設不經過坐標原點且斜率為的直線交橢圓: 于點、，點滿足. 若點在橢圓上，則四邊形OPRQ(或)的面積為定值。