
【題目】某體育公司對最近6個月內的市場占有率進行了統計,結果如表:

(1)可用線性回歸模型擬合![]() 與
與![]() 之間的關系嗎?如果能,請求出
之間的關系嗎?如果能,請求出![]() 關于
關于![]() 的線性回歸方程,如果不能,請說明理由;
的線性回歸方程,如果不能,請說明理由;
(2)公司決定再采購![]() ,
,![]() 兩款車擴大市場,
兩款車擴大市場,![]() ,
,![]() 兩款車各100輛的資料如表:
兩款車各100輛的資料如表:

平均每輛車每年可為公司帶來收入500元,不考慮采購成本之外的其他成本,假設每輛車的使用壽命都是整數年,用每輛車使用壽命的頻率作為概率,以每輛車產生利潤的期望值作為決策依據,應選擇采購哪款車型?
參考數據:![]() ,
,![]() ,
,![]() ,
,![]() .
.
參考公式:相關系數 ;
;
回歸直線方程![]() ,其中
,其中 ,
,![]() .
.
 孟建平小學滾動測試系列答案
孟建平小學滾動測試系列答案 黃岡天天練口算題卡系列答案
黃岡天天練口算題卡系列答案科目:高中數學 來源: 題型:
【題目】為了緩解日益擁堵的交通狀況,不少城市實施車牌競價策略,以控制車輛數量.某地車牌競價的基本規則是:①“盲拍”,即所有參與競拍的人都要網絡報價一次,每個人不知曉其他人的報價,也不知道參與當期競拍的總人數;②競價時間截止后,系統根據當期車牌配額,按照競拍人的出價從高到低分配名額.某人擬參加2018年5月份的車牌競拍,他為了預測最低成交價,根據競拍網站的數據,統計了最近5個月參與競拍的人數(見下表):

(1)由收集數據的散點圖發現,可用線性回歸模型擬合競拍人數y(萬人)與月份編號t之間的相關關系.請用最小二乘法求y關于t的線性回歸方程:![]() ,并預測2018年5月份參與競拍的人數.
,并預測2018年5月份參與競拍的人數.
(2)某市場調研機構從擬參加2018年5月份車牌競拍人員中,隨機抽取了200人,對他們的擬報價價格進行了調查,得到如下頻數分布表和頻率分布直方圖:

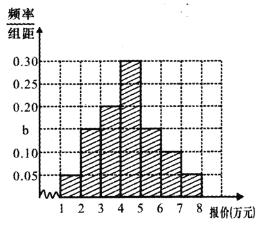
(i)求![]() 的值及這200位竟拍人員中報價大于5萬元的人數;
的值及這200位竟拍人員中報價大于5萬元的人數;
(ii)若2018年5月份車牌配額數量為3000,假設競拍報價在各區間分布是均勻的,請你根據以上抽樣的數據信息,預測(需說明理由)競拍的最低成交價.
參考公式及數據:①![]() ,其中
,其中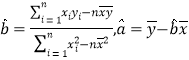 ;
;
②![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知平面直角坐標系![]() 中,過點
中,過點![]() 的直線l的參數方程為
的直線l的參數方程為![]() (t為參數),以原點O為極點,x軸的正半軸為極軸建立極坐標系,曲線C的極坐標方程為
(t為參數),以原點O為極點,x軸的正半軸為極軸建立極坐標系,曲線C的極坐標方程為![]() 與曲線C相交于不同的兩點M,N.
與曲線C相交于不同的兩點M,N.
(1)求曲線C的直角坐標方程和直線l的普通方程;
(2)若![]() ,求實數a的值.
,求實數a的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】選修4-4:坐標系與參數方程
在直角坐標系![]() 中,曲線
中,曲線![]() 的參數方程為
的參數方程為![]() (
(![]() 為參數),以原點
為參數),以原點![]() 為極點,
為極點,![]() 軸的非負半軸為極軸建立極坐標系,曲線
軸的非負半軸為極軸建立極坐標系,曲線![]() 的極坐標方程為
的極坐標方程為![]() .
.
(1)寫出曲線![]() 的極坐標方程和曲線
的極坐標方程和曲線![]() 的直角坐標方程;
的直角坐標方程;
(2)已知點![]() 是曲線
是曲線![]() 上一點,點
上一點,點![]() 是曲線
是曲線![]() 上一點,
上一點,![]() 的最小值為
的最小值為![]() ,求實數
,求實數![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】從某工廠的一個車間抽取某種產品![]() 件,產品尺寸(單位:
件,產品尺寸(單位:![]() )落在各個小組的頻數分布如下表:
)落在各個小組的頻數分布如下表:
數據分組 |
|
|
|
|
|
|
|
頻數 |
|
|
|
|
|
|
|
(1)根據頻數分布表,求該產品尺寸落在![]() 的概率;
的概率;
(2)求這![]() 件產品尺寸的樣本平均數
件產品尺寸的樣本平均數![]() ;(同一組中的數據用該組區間的中點值作代表)
;(同一組中的數據用該組區間的中點值作代表)
(3)根據頻數分布對應的直方圖,可以認為這種產品尺寸![]() 服從正態分布
服從正態分布![]() ,其中
,其中![]() 近似為樣本平均值
近似為樣本平均值![]() ,
,![]() 近似為樣本方差
近似為樣本方差![]() ,經過計算得
,經過計算得![]() ,利用該正態分布,求
,利用該正態分布,求![]() .
.
附:①若隨機變量![]() 服從正態分布
服從正態分布![]() ,則
,則![]() ,
,![]() ;②
;②![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() :
:![]() 的左、右焦點為
的左、右焦點為![]() ,
,![]() ,點
,點![]() 在橢圓
在橢圓![]() 上,且
上,且![]() 面積的最大值為
面積的最大值為![]() ,周長為6.
,周長為6.
(1)求橢圓![]() 的方程,并求橢圓
的方程,并求橢圓![]() 的離心率;
的離心率;
(2)已知直線![]() :
:![]() 與橢圓
與橢圓![]() 交于不同的兩點
交于不同的兩點![]() ,若在
,若在![]() 軸上存在點
軸上存在點![]() ,使得
,使得![]() 與
與![]() 中點的連線與直線
中點的連線與直線![]() 垂直,求實數
垂直,求實數![]() 的取值范圍
的取值范圍
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】選修4-4:坐標系與參數方程
已知在極坐標系中,點![]() ,
,![]() ,
,![]() 是線段
是線段![]() 的中點,以極點為原點,極軸為
的中點,以極點為原點,極軸為![]() 軸的正半軸,并在兩坐標系中取相同的長度單位,建立平面直角坐標系,曲線
軸的正半軸,并在兩坐標系中取相同的長度單位,建立平面直角坐標系,曲線![]() 的參數方程是
的參數方程是![]() (
(![]() 為參數).
為參數).
(1)求點![]() 的直角坐標,并求曲線
的直角坐標,并求曲線![]() 的普通方程;
的普通方程;
(2)設直線![]() 過點
過點![]() 交曲線
交曲線![]() 于
于![]() 兩點,求
兩點,求![]() 的值.
的值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com