
科目: 來源: 題型:
【題目】綜合與實踐﹣四邊形旋轉中的數學
“智慧”數學小組在課外數學活動中研究了一個問題,請幫他們解答.
任務一:如圖1,在矩形ABCD中,AB=6,AD=8,E,F分別為AB,AD邊的中點,四邊形AEGF為矩形,連接CG.
(1)請直接寫出CG的長是______.
(2)如圖2,當矩形AEGF繞點A旋轉(比如順時針旋轉)至點G落在邊AB上時,請計算DF與CG的長,通過計算,試猜想DF與CG之間的數量關系.
(3)當矩形AEGF繞點A旋轉至如圖3的位置時,(2)中DF與CG之間的數量關系是否還成立?請說明理由.
任務二:“智慧”數學小組對圖形的旋轉進行了拓展研究,如圖4,在ABCD中,∠B=60°,AB=6,AD=8,E,F分別為AB,AD邊的中點,四邊形AEGF為平行四邊形,連接CG.“智慧”數學小組發現DF與CG仍然存在著特定的數量關系.
(4)如圖5,當AEGF繞點A旋轉(比如順時針旋轉),其他條件不變時,“智慧”數學小組發現DF與CG仍然存在著這一特定的數量關系.請你直接寫出這個特定的數量關系.





查看答案和解析>>
科目: 來源: 題型:
【題目】綜合與探究
問題情境
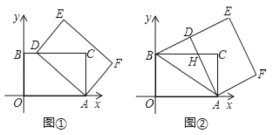
在綜合實踐課上,老師讓同學們探究“平面直角坐標系中的旋轉問題”.如圖,在平面直角坐標系中,四邊形![]() 是矩形,點
是矩形,點![]() ,點
,點![]() ,點
,點![]() .
.
操作發現
以點![]() 為中心,順時針旋轉矩形
為中心,順時針旋轉矩形![]() ,得到矩形
,得到矩形![]() ,點
,點![]() ,
,![]() ,
,![]() 的對應點分別為
的對應點分別為![]() ,
,![]() ,
,![]() .
.
(1)如圖①,當點![]() 落在
落在![]() 邊上時,求點
邊上時,求點![]() 的坐標;
的坐標;
繼續探究
(2)如圖②,當點![]() 落在線段
落在線段![]() 上時,
上時,![]() 與
與![]() 交于點
交于點![]() .
.
①求證![]() ;
;
②求點![]() 的坐標.
的坐標.
拓展探究
(3)如圖①,點![]() 是
是![]() 軸上任意一點,點
軸上任意一點,點![]() 是平面內任意一點,是否存在點
是平面內任意一點,是否存在點![]() 使以
使以![]() 、
、![]() 、
、![]() 、
、![]() 為頂點的四邊形是菱形?若存在,請直接寫出點
為頂點的四邊形是菱形?若存在,請直接寫出點![]() 的坐標;若不存在,請說明理由.
的坐標;若不存在,請說明理由.
查看答案和解析>>
科目: 來源: 題型:
【題目】請閱讀下列材料,并完成相應的任務.
在數學中,當問題的條件不夠時間,常添加輔助線構成新圖形,形成新關系,建立已知與未知的橋梁,從而把原問題轉化為易于解決的問題.在著名美籍匈牙利數學教波利亞所著的《數學的發現》一書中有這樣一個例子:試作一個三角形,使它的三邊長分別是各條中線長的三分之一,解決這個問題的步驟如下:

第一步,如圖1,己知![]() 的三條中線
的三條中線![]() ,
,![]() 和
和![]() 相交于點
相交于點![]() ,則有
,則有![]() .
.
下面是該結論的部分證明過程:

證明:如圖1,過點![]() 作
作![]() 的平分線,交
的平分線,交![]() 的延長線于點
的延長線于點![]() ,則
,則![]() .
.
又![]() ,
,
∴![]() .
.
∴![]() .
.
∵點![]() 是
是![]() 的中點,
的中點,
∴![]() .
.
……
第二步,同理可以證明:![]() .
.
第三步,如圖2,取BM的中點![]() ,連接
,連接![]() .則
.則![]() 的三邊長分別是各條中線長的三分之一.
的三邊長分別是各條中線長的三分之一.
任務:(1)請在上面第一步中證明過程的基礎上完成對結論![]() 的證明;
的證明;
(2)請完成第三步的結論的證明;
(3)請直接寫出圖2中![]() 與
與![]() 的面積比:
的面積比:![]() _______.
_______.
查看答案和解析>>
科目: 來源: 題型:
【題目】從共享單車,共享汽車等共享出行到共享充電寶,共享雨傘等共享物品,各式各樣的共享經濟模式在各個領域迅速普及應用,越來越多的企業與個人成為參與者與受益者.小宇和小強分別對共享經濟中的“共享出行”和“共享知識”最感興趣,他們上網查閱了相關資料,順便收集到四個共享經濟領域的圖標,并將其制成編號為![]() ,
,![]() ,
,![]() ,
,![]() 的四張卡片(除編號和內容外,其余完全相同)他們將這四張卡片背面朝上,洗勻放好,從中隨機抽取一張(不放回),再從中隨機抽取一張,請用列表或畫樹狀圖的方法求抽到的兩張卡片恰好是“共享出行”和“共享知識”的概率(這四張卡片分別用它們的編號
的四張卡片(除編號和內容外,其余完全相同)他們將這四張卡片背面朝上,洗勻放好,從中隨機抽取一張(不放回),再從中隨機抽取一張,請用列表或畫樹狀圖的方法求抽到的兩張卡片恰好是“共享出行”和“共享知識”的概率(這四張卡片分別用它們的編號![]() ,
,![]() ,
,![]() ,
,![]() 表示)
表示)

查看答案和解析>>
科目: 來源: 題型:
【題目】某文具專柜從太原市小商品批發市場購進一批膠帶,每個進價0.5元.調查發現,當銷售價為0.8元時,每月可售出500個;如果售價每降低0.05元,那么平均每月可多售出200個.
(1)當降價0.2元時,平均每月銷售膠帶______個;
(2)攤主要想平均每月贏利180元,且盡可能讓利與顧客,應該如何定價?
(3)在(2)的條件下,每個膠帶的利潤率是______.
查看答案和解析>>
科目: 來源: 題型:
【題目】如圖,在△ABC 中,點 D 是邊 BC 上的點(與 B、C 兩點不重合),過點 D作 DE∥AC,DF∥AB,分別交 AB、AC 于 E、F 兩點,下列說法正確的是( )

A. 若 AD 平分∠BAC,則四邊形 AEDF 是菱形
B. 若 BD=CD,則四邊形 AEDF 是菱形
C. 若 AD 垂直平分 BC,則四邊形 AEDF 是矩形
D. 若 AD⊥BC,則四邊形 AEDF 是矩形
查看答案和解析>>
科目: 來源: 題型:
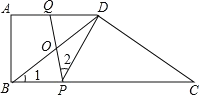
【題目】如圖,在ABCD中,AD∥BC,∠A=90°,BD=DC,AB=6,AD=8,點P、Q分別為BC、AD上的動點,連接PQ,與BD相交于點O.
(1)當∠1=∠2時,求證:∠DOQ=∠DPC;
(2)當(1)的條件下,求證:DQ·PC=BD·DO;
(3)如果點P由點B向點C移動,每秒移動2個單位,同時點Q由點D向點A移動,每秒移動1個單位,設移動的時間為t秒,是否存在某一時刻,使得△BOP為直角三角形,如果存在,請直接寫出t的值;如果不存在,請說明理由.
查看答案和解析>>
科目: 來源: 題型:
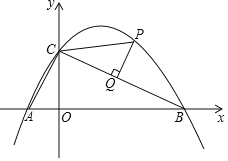
【題目】如圖,二次函數![]() 的圖像與
的圖像與![]() 軸相交于點A(-1,0),B(4,0),與
軸相交于點A(-1,0),B(4,0),與![]() 軸相交于點C.
軸相交于點C.
(1)求該函數的表達式;
(2)若點P(2,m)為該函數在第一象限內的圖象上一點,過點P作PQ⊥BC,垂足為點Q,連接PC,求線段PQ的長;
(3)在(2)的條件下,點M為該函數圖象上一點,且∠MAP=45°,求點M的坐標.

查看答案和解析>>
科目: 來源: 題型:
【題目】(9分)九年級數學興趣小組經過市場調查,得到某種運動服每月的銷量與售價的相關信息如下表:
售價(元/件) | 100 | 110 | 120 | 130 | … |
月銷量(件) | 200 | 180 | 160 | 140 | … |
已知該運動服的進價為每件60元,設售價為![]() 元.
元.
(1)請用含x的式子表示:①銷售該運動服每件的利潤是 元;②月銷量是 件;(直接寫出結果)
(2)設銷售該運動服的月利潤為![]() 元,那么售價為多少時,當月的利潤最大,最大利潤是多少?
元,那么售價為多少時,當月的利潤最大,最大利潤是多少?
查看答案和解析>>
科目: 來源: 題型:
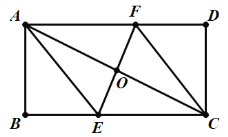
【題目】如圖,矩形ABCD中,AB=4,BC=8,過對角線AC中點O的直線分別交BC、AD邊于點E、F.
(1)求證:四邊形AECF是平行四邊形;
(2)當四邊形AECF是菱形時,求AF的長.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com