
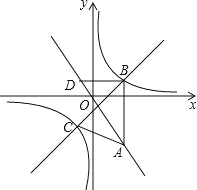
【題目】如圖,在平面直角坐標系xOy中,點A(a,﹣![]() )在直線y=﹣
)在直線y=﹣![]() 上,AB∥y軸,且點B的縱坐標為1,雙曲線y=
上,AB∥y軸,且點B的縱坐標為1,雙曲線y=![]() 經過點B.
經過點B.
(1)求a的值及雙曲線y=![]() 的解析式;
的解析式;
(2)經過點B的直線與雙曲線y=![]() 的另一個交點為點C,且△ABC的面積為
的另一個交點為點C,且△ABC的面積為![]() .
.
①求直線BC的解析式;
②過點B作BD∥x軸交直線y=﹣![]() 于點D,點P是直線BC上的一個動點.若將△BDP以它的一邊為對稱軸進行翻折,翻折前后的兩個三角形所組成的四邊形為正方形,直接寫出所有滿足條件的點P的坐標.
于點D,點P是直線BC上的一個動點.若將△BDP以它的一邊為對稱軸進行翻折,翻折前后的兩個三角形所組成的四邊形為正方形,直接寫出所有滿足條件的點P的坐標.
【答案】(1)y=![]() (2)①y=x-1②(﹣1,﹣2)或(
(2)①y=x-1②(﹣1,﹣2)或(![]() ,-
,-![]() )
)
【解析】
試題(1)根據一次函數圖象上點的坐標特征可得到![]() 解得a=2,則A(2,-
解得a=2,則A(2,-![]() )),再確定點B的坐標為(2,1),然后把B點坐標代入
)),再確定點B的坐標為(2,1),然后把B點坐標代入![]() 中求出m的值即可得到反比例函數的解析式;
中求出m的值即可得到反比例函數的解析式;
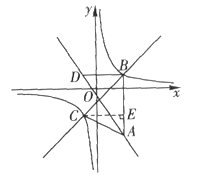
(2)①過點C作CE⊥AB于點E,如圖5.,根據三角形面積公式得到![]() 解得CE=3,點C的橫坐標為-1.
解得CE=3,點C的橫坐標為-1.
∵點C在雙曲線![]() 上,則點C的坐標為(-1,-2),再利用待定系數法求直線BC的解析式;②先確定D(-1,1),根據直線BC解析式的特征可得直線BC與x軸的夾角為45°,而BD∥x軸,于是得到∠DBC=45°,根據正方形的判定方法,只有△PBD為等腰直角三角形時,以它的一邊為對稱軸進行翻折,翻折前后的兩個三角形所組成的四邊形為正方形,分類討論:若∠BPD=90°,則點P在BD的垂直平分線上,易得此時P(
上,則點C的坐標為(-1,-2),再利用待定系數法求直線BC的解析式;②先確定D(-1,1),根據直線BC解析式的特征可得直線BC與x軸的夾角為45°,而BD∥x軸,于是得到∠DBC=45°,根據正方形的判定方法,只有△PBD為等腰直角三角形時,以它的一邊為對稱軸進行翻折,翻折前后的兩個三角形所組成的四邊形為正方形,分類討論:若∠BPD=90°,則點P在BD的垂直平分線上,易得此時P(![]() ,-
,-![]() );若∠BDP=90°,利用PD∥y軸,易得此時P(-1,-2).
);若∠BDP=90°,利用PD∥y軸,易得此時P(-1,-2).
試題解析:(1)∵點A![]() 在直線
在直線![]() 上,
上,
∴![]() .
.
∴![]() .…………………………1分
.…………………………1分
∵AB∥y軸,且點B的縱坐標為1,
∴點B的坐標為(2,1).
∵雙曲線![]() 經過點B(2,1),
經過點B(2,1),
∴![]() ,即
,即![]() .
.
∴反比例函數的解析式為![]() .
.
(2)①過點C作CE⊥AB于點E,如圖.
∴![]() .
.
∴CE="3."
∴點C的橫坐標為-1.
∵點C在雙曲線![]() 上,
上,
∴點C的坐標為(-1,-2).
設直線BC的解析式為![]() ,
,
則![]() 解得
解得![]()
∴直線BC的解析式為![]() .
.
②(-1,-2)或![]() .
.


科目:初中數學 來源: 題型:
【題目】如圖,反比例函數y=![]() (k>0)與矩形OABC在第一象限相交于D、E兩點,OA=2,OC=4,連接OD、OE、DE.記△OAD、△OCE的面積分別為S、S .
(k>0)與矩形OABC在第一象限相交于D、E兩點,OA=2,OC=4,連接OD、OE、DE.記△OAD、△OCE的面積分別為S、S .
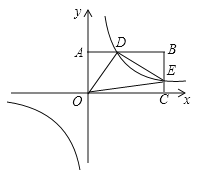
(1)①點B的坐標為 ;②S S(填“>”、“<”、“=”);
(2)當點D為線段AB的中點時,求k的值及點E的坐標;
(3)當S+S=2時,試判斷△ODE的形狀,并求△ODE的面積.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】(本小題滿分10分 )在端午節前夕三位同學到某超市調研一種進價為2元的粽子的售銷情況,請跟據小麗提供的信息,解答小華和小明提出的問題
小麗:每個定價3元,每天能賣出500個,而且,這種粽子每上漲0.1元,其售銷量將減小10個
小華:照你所說,如果實現每天800元的售銷利潤,那該如何定價?莫忘了物價局規定售價不能超過進價的240%喲
小明:800元售銷利潤是不是最多的呢?如果不是,那該如何定價,才會使每天的利潤最大?.
(1)小華的問題解答:
(2)小明的問題解答:
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某市為了鼓勵居民在枯水期(當年11月至第二年5月)節約用電,規定7:00至23:00為用電高峰期,此期間用電電費y1(單位:元)與用電量x(單位:度)之間滿足的關系如圖所示;規定23:00至第二天早上7:00為用電低谷期,此期間用電電費y2(單位:元)與用電量x(單位:元)之間滿足如表所示的一次函數關系.
(1)求y2與x的函數關系式;并直接寫出當0≤x≤180和x>180時,y1與x的函數關系式;

(2)若市民王先生一家在12月份共用電350度,支付電費150元,求王先生一家在高峰期和低谷期各用電多少度.
低谷期用電量x度 | … | 80 | 100 | 140 | … |
低谷期用電電費y2元 | … | 20 | 25 | 35 | … |
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知正比例函數和反比例函數的圖象都經過點A(﹣3,﹣3).
(1)求正比例函數和反比例函數的表達式;
(2)把直線OA向上平移后與反比例函數的圖象交于點B(﹣6,m),與x軸交于點C,求m的值和直線BC的表達式;
(3)在(2)的條件下,直線BC與y軸交于點D,求以點A,B,D為頂點的三角形的面積;
(4)在(3)的條件下,點A,B,D在二次函數的圖象上,試判斷該二次函數在第三象限內的圖象上是否存在一點E,使四邊形OECD的面積S1與四邊形OABD的面積S滿足:S1=![]() S?若存在,求點E的坐標;若不存在,請說明理由.
S?若存在,求點E的坐標;若不存在,請說明理由.

查看答案和解析>>
科目:初中數學 來源: 題型:
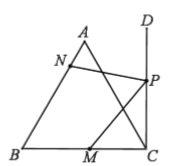
【題目】如圖,點![]() 在等邊
在等邊![]() 的邊
的邊![]() 上,
上,![]() ,射線
,射線![]() ,垂足為點
,垂足為點![]() ,點
,點![]() 是射線
是射線![]() 上一動點,點
上一動點,點![]() 是線段
是線段![]() 上一動點,當
上一動點,當![]() 的值最小時,
的值最小時,![]() ,則
,則![]() 的長為___________________.
的長為___________________.
查看答案和解析>>
科目:初中數學 來源: 題型:
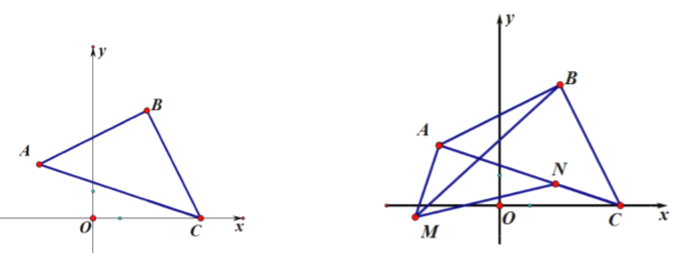
【題目】如圖,等腰直角三角形![]() 中,
中,![]() ,
,![]() ,
,![]() 點坐標為
點坐標為![]() ,
,![]() 點坐標為
點坐標為![]() ,且
,且 ![]() ,
,![]() 滿足
滿足![]() .
.
(1)寫出![]() 、
、![]() 兩點坐標;
兩點坐標;
(2)求![]() 點坐標;
點坐標;
(3)如圖,![]() ,
,![]() 為
為![]() 上一點,且
上一點,且![]() ,請寫出線段
,請寫出線段![]() 的數量關系,并說明理由.
的數量關系,并說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】平面直角坐標系xOy中(如圖),已知拋物線y=ax2+bx+3與y軸相交于點C,與x軸正半軸相交于點A,OA=OC,與x軸的另一個交點為B,對稱軸是直線x=1,頂點為P.
(1)求這條拋物線的表達式和頂點P的坐標;
(2)拋物線的對稱軸與x軸相交于點M,求∠PMC的正切值;
(3)點Q在y軸上,且△BCQ與△CMP相似,求點Q的坐標.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】拋物線y=x2+(m﹣3)x﹣m+2的圖象交x軸正半軸于點A,交x軸負半軸于點B,交y軸于點C.
(1)求m的取值范圍;
(2)若△ABC恰為等腰三角形,求m.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com