
【題目】如圖所示,直線![]() 與反比例函數
與反比例函數![]() 的圖象交于點
的圖象交于點![]() ,
,![]() ,與坐標軸交于A、B兩點.
,與坐標軸交于A、B兩點.
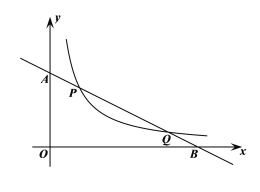
(1)求一次函數與反比例函數的解析式;
(2)觀察圖象,當![]() 時,直接寫出不等式
時,直接寫出不等式![]() 的解集;
的解集;
(3)將直線![]() 向下平移
向下平移![]() 個單位,若直線與反比例函數
個單位,若直線與反比例函數![]() 的圖象有唯一交點,求
的圖象有唯一交點,求![]() 的值.
的值.
【答案】(1)![]() ,
,![]() ;(2)
;(2)![]() 或
或![]() ;(3)
;(3)![]() 的值為1.
的值為1.
【解析】
(1)把點![]() 代入
代入![]() 求得m=8,從而求出反比例函數解析式,再把P(2,a)代入
求得m=8,從而求出反比例函數解析式,再把P(2,a)代入![]() 求得a=8,最后把P(2,4),Q(8,1)代入
求得a=8,最后把P(2,4),Q(8,1)代入![]() ,求出k和b的值即可;
,求出k和b的值即可;
(2)根據兩函數交點坐標結合圖象即可得出不等式![]() 的解集;
的解集;
(3)平移后的直線解析式與反比例函數解析式聯立方程組,根據兩函數圖象有唯一交點,得△=0,求解方程即可.
(1)把![]() 代入
代入![]() 得:
得:
![]()
∴反比例函數的解析式為![]() .
.
把![]() 代入
代入![]() 得:
得:
![]()
∴![]()
把![]() ,
,![]() 分別代入
分別代入![]() 得:
得:
![]() ,解之得:
,解之得: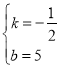
∴一次函數的解析式為![]() ;
;
(2)∵兩函數圖象的交點為![]() ,
,![]()
觀察圖象得,當![]() 或
或![]() 時,
時,![]() ;
;
(3)將直線![]() 向下平移
向下平移![]() 個單位后,直線的解析式為
個單位后,直線的解析式為![]()
∵直線![]() 與雙曲線
與雙曲線![]()
![]() 有唯一交點
有唯一交點
∴方程![]() 有唯一解
有唯一解
整理得:![]()
∴![]()
解之得:![]() (舍去).
(舍去).
∴![]() 的值為1.
的值為1.


科目:初中數學 來源: 題型:
【題目】某水果店計劃購進甲、乙兩種高檔水果共400千克,每千克的售價、成本與購進數量(千克)之間關系如表:
每千克售價(元) | 每千克成本(元) | |
甲 | ﹣0.1x+100 | 50 |
乙 | ﹣0.2x+120(0<x≤200) | 60 |
|
(1)若甲、乙兩種水果全部售完,求水果店獲得總利潤y(元)與購進乙種水果x(千克)之間的函數關系式(其他成本不計);
(2)若購進兩種水果都不少于100千克,當兩種水果全部售完,水果能獲得的最大利潤.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系中有一個3×3的正方形網格,其右下角格點(小正方形的頂點)A的坐標為(﹣1,1),左上角格點B的坐標為(﹣4,4),若分布在過定點(﹣1,0)的直線y=﹣k(x+1)兩側的格點數相同,則k的取值可以是( )

A.![]() B.
B.![]() C.2D.
C.2D.![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】二次函數![]() 的函數圖象如圖,點
的函數圖象如圖,點![]() 位于坐標原點,點
位于坐標原點,點![]() 在
在![]() 軸的正半軸上,點
軸的正半軸上,點![]() 在二次函數
在二次函數![]() 位于第一象限的圖象上,
位于第一象限的圖象上,![]() ,
,![]() ,
,![]() ,
,![]() …都是直角頂點在拋物線上的等腰直角三角形,則
…都是直角頂點在拋物線上的等腰直角三角形,則![]() 的斜邊長為( )
的斜邊長為( )

A.20B.![]() C.22D.
C.22D.![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某企業復工之后,舉行了一個簡單的技工比賽,參賽的五名選手在單位時間內加工零件的合格率分別為:94.3% ,96.1% , 94.3% ,91.7% ,93.5%.關于這組數據,下列說法正確的是( )
A.平均數是93.96%B.方差是0
C.中位數是93.5%D.眾數是94.3%
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某縣教育局為了豐富初中學生的大課間活動,要求各學校開展形式多樣的陽光體育活動.某中學就“學生體育活動興趣愛好”的問題,隨機調查了本校某班的學生,并根據調查結果繪制成如下的不完整的扇形統計圖和條形統計圖:
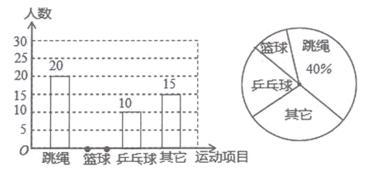
(1)在這次調查中,共調查了 人,在扇形統計圖中,“乒乓球”的百分比為 %,如果學校有800名學生,估計全校學生中有 人喜歡籃球項目;
(2)請將條形統計圖補充完整;
(3)學校在喜歡籃球的初一學生中挑選了3名同學,分別是李明、林海和陳陽,然后在這3名學生中最終挑選2人參加學校的籃球隊,請用列表法或畫樹狀圖的方法求出李明最終被選上的概率.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】(本小題滿分12分)
已知:把Rt△ABC和Rt△DEF按如圖(1)擺放(點C與點E重合),點B、C(E)、F在同一條直線上.∠ACB = ∠EDF = 90°,∠DEF = 45°,AC = 8 cm,BC = 6 cm,EF = 9 cm.
如圖(2),△DEF從圖(1)的位置出發,以1 cm/s的速度沿CB向△ABC勻速移動,在△DEF移動的同時,點P從△ABC的頂點B出發,以2 cm/s的速度沿BA向點A勻速移動.當△DEF的頂點D移動到AC邊上時,△DEF停止移動,點P也隨之停止移動.DE與AC相交于點Q,連接PQ,設移動時間為t(s)(0<t<4.5).
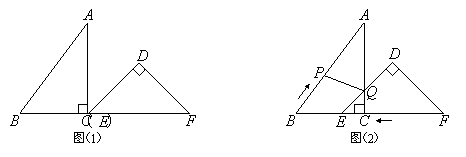
解答下列問題:
(1)當t為何值時,點A在線段PQ的垂直平分線上?
(2)連接PE,設四邊形APEC的面積為y(cm2),求y與t之間的函數關系式;是否存在某一時刻t,使面積y最小?若存在,求出y的最小值;若不存在,說明理由.
(3)是否存在某一時刻t,使P、Q、F三點在同一條直線上?若存在,求出此時t的值;若不存在,說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,△ABC內接于⊙O,∠CBG=∠A,CD為直徑,OC與AB相交于點E,過點E作EF⊥BC,垂足為F,延長CD交GB的延長線于點P,連接BD.
(1)求證:PG與⊙O相切;
(2)若![]() =
=![]() ,求
,求![]() 的值;
的值;
(3)在(2)的條件下,若⊙O的半徑為8,PD=OD,求OE的長.

查看答案和解析>>
科目:初中數學 來源: 題型:
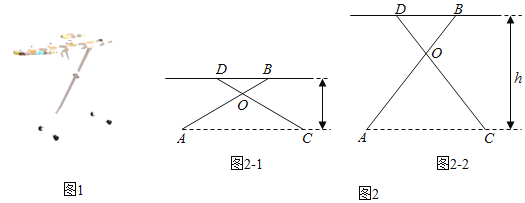
【題目】有一種升降熨燙臺如圖1所示,其原理是通過改變兩根支撐桿夾角的度數來調整熨燙臺的高度.圖2是這種升降熨燙臺的平面示意圖.AB和CD是兩根相同長度的活動支撐桿,點O是它們的連接點,OA=OC,h(cm)表示熨燙臺的高度.
(1)如圖2﹣1.若AB=CD=110cm,∠AOC=120°,求h的值;
(2)愛動腦筋的小明發現,當家里這種升降熨燙臺的高度為120cm時,兩根支撐桿的夾角∠AOC是74°(如圖2﹣2).求該熨燙臺支撐桿AB的長度(結果精確到lcm).
(參考數據:sin37°≈0.6,cos37°≈0.8,sin53°≈0.8,cos53°≈0.6.)
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com