
【題目】閱讀下列材料:
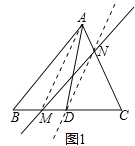
小明遇到一個問題:AD是△ABC的中線, 點M為BC邊上任意一點(不與點D重合),過點M作一直線,使其等分△ABC的面積.
他的做法是:如圖1,連結AM,過點D作DN//AM交AC于點N,作直線MN,直線MN即為所求直線.
請你參考小明的做法,解決下列問題:
(1)如圖2, AE等分四邊形ABCD的面積,M為CD邊上一點,過M作一直線MN,使其等分四邊形ABCD的面積(要求:在圖2中畫出直線MN,并保留作圖痕跡);
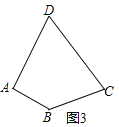
(2)如圖3,求作過點A的直線AE,使其等分四邊形ABCD的面積(要求:在圖3中畫出直線AE,并保留作圖痕跡).

 習題精選系列答案
習題精選系列答案科目:初中數學 來源: 題型:
【題目】已知k是不等于0的常數,反比例函數與二次函數在同一坐標系的大致圖象如圖,則它們的解析式可能分別是( ) 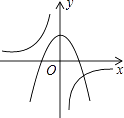
A.y=﹣ ![]() ,y=﹣kx2+k
,y=﹣kx2+k
B.y= ![]() ,y=﹣kx2+k
,y=﹣kx2+k
C.y= ![]() ,y=kx2+k
,y=kx2+k
D.y=﹣ ![]() ,y=﹣kx2﹣k
,y=﹣kx2﹣k
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖所示,O為直線AB上一點,OC平分∠AOE,∠DOE=90°,則以下結論正確的有____________.(只填序號)
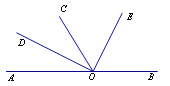
①∠AOD與∠BOE互為余角;
②OD平分∠COA;
③∠BOE=56°40′,則∠COE=61°40′;
④∠BOE=2∠COD.
查看答案和解析>>
科目:初中數學 來源: 題型:
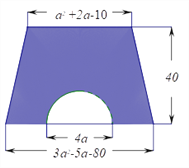
【題目】如圖,梯形的上底為![]() +2
+2![]() -10,下底為3
-10,下底為3![]() -5
-5![]() -80,高為40.(
-80,高為40.(![]() 取3)
取3)
(1)用式子表示圖中陰影部分的面積;
(2)當![]() =10時,求陰影部分面積的值。
=10時,求陰影部分面積的值。
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】同學們都知道,|5﹣(﹣2)|表示5與﹣2之差的絕對值,實際上也可理解為5與﹣2兩數在數軸上所對的兩點之間的距離.試探索:
(1)求|5﹣(﹣2)|=________.
(2)數軸上表示x和﹣1的兩點之間的距離表示為________.
(3)找出所有符合條件的整數x,使|x+5|+|x﹣2|=7,這樣的整數有________個.
查看答案和解析>>
科目:初中數學 來源: 題型:
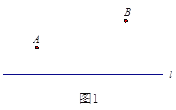
【題目】問題:如圖1,點![]() ,
,![]() 在直線
在直線![]() 的同側,在直線
的同側,在直線![]() 上找一點
上找一點![]() ,使得
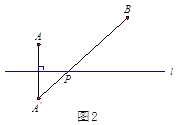
,使得![]() 的值最小.小明的思路是:如圖2,作點
的值最小.小明的思路是:如圖2,作點![]() 關于直線
關于直線![]() 的對稱點
的對稱點![]() ,連接
,連接![]() ,則
,則![]() 與直線
與直線![]() 的交點
的交點![]() 即為所求.
即為所求.
請你參考小明同學的思路,探究并解決下列問題:
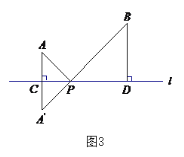
(1)如圖3,在圖2的基礎上,設![]() 與直線
與直線![]() 的交點為
的交點為![]() ,過點
,過點![]() 作
作![]() ,垂足為
,垂足為![]() . 若
. 若![]() ,
,![]() ,
,![]() ,寫出
,寫出![]() 的值為____________;
的值為____________;
(2)將(1)中的條件“![]() ”去掉,換成“
”去掉,換成“![]() ”,其它條件不變,寫出此時
”,其它條件不變,寫出此時![]() 的值 ___________;
的值 ___________;
(3)求![]() +
+![]() 的最小值.
的最小值.
查看答案和解析>>
科目:初中數學 來源: 題型:
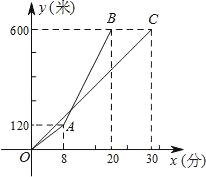
【題目】甲、乙兩人沿同一路線登山,圖中線段OC、折線OAB分別是甲、乙兩人登山的路程y(米)與登山時間x(分)之間的函數圖象.請根據圖象所提供的信息,解答如下問題:
(1)求甲登山的路程與登山時間之間的函數關系式,并寫出自變量x的取值范圍;
(2)求乙出發后多長時間追上甲?此時乙所走的路程是多少米?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】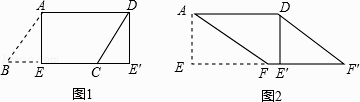
(1)如圖1所示,平行四邊形紙片ABCD中,AD=5,SABCD=15,過點A作AE⊥BC,垂足為E,沿AE剪下△ABE,將它平移至△DCE′的位置,拼成四邊形AEE′D,則四邊形AEE′D是形.
(2)如圖2所示,在(1)中的四邊形紙片AEE′D中,在EE′上取一點F,使EF=4,剪下△AEF,將它平移至△DE′F′的位置,拼成四邊形AFF′D.
①求證:四邊形AFF′D是菱形;
②求四邊形AFF′D兩條對角線的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在△ABC中,AB=BC,D是AC中點,BE平分∠ABD交AC于點E,點O是AB上一點,⊙O過B、E兩點,交BD于點G,交AB于點F. 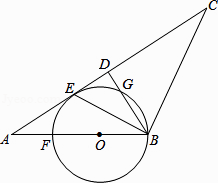
(1)判斷直線AC與⊙O的位置關系,并說明理由;
(2)當BD=6,AB=10時,求⊙O的半徑.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com