
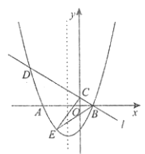
【題目】如圖,已知拋物線![]() 與
與![]() 軸交于點
軸交于點![]() 、
、![]() (點
(點![]() 在點
在點![]() 的左側),經過點
的左側),經過點![]() 的直線
的直線![]() :
:![]() 與
與![]() 軸交于點
軸交于點![]() ,與拋物線的另一個交點為
,與拋物線的另一個交點為![]() .
.
(1)則點![]() 的坐標為__________,點
的坐標為__________,點![]() 的坐標為__________,拋物線的對稱軸為__________;
的坐標為__________,拋物線的對稱軸為__________;
(2)點![]() 是直線
是直線![]() 下方拋物線上的一點,當
下方拋物線上的一點,當![]() 時.求
時.求![]() 面積的最大值;
面積的最大值;
(3)設![]() 為拋物線對稱軸上一點,點
為拋物線對稱軸上一點,點![]() 在拋物線上,若以點
在拋物線上,若以點![]() 、
、![]() 、
、![]() 、
、![]() 為頂點的四邊形為矩形,求
為頂點的四邊形為矩形,求![]() 的值.
的值.
【答案】(1)![]() ,
,![]() ,拋物線的對稱軸是:直線
,拋物線的對稱軸是:直線![]() ;(2)當
;(2)當![]() 時,
時,![]() 面積的最大值為
面積的最大值為![]() ;(3)當點
;(3)當點![]() 、
、![]() 、
、![]() 、
、![]() 為頂點的四邊形為矩形時,
為頂點的四邊形為矩形時,![]() 的值為
的值為![]() ,
,![]()
【解析】
(1)利用拋物線與![]() 軸交點的縱坐標為
軸交點的縱坐標為![]() ,列方程直接求解,利用拋物線的對稱軸公式直接求對稱軸方程;
,列方程直接求解,利用拋物線的對稱軸公式直接求對稱軸方程;
(2)過點![]() 作
作![]() 軸交直線
軸交直線![]() 于點
于點![]() ,利用
,利用![]() ,建立面積與
,建立面積與![]() 的橫坐標的函數,利用函數的性質求最大值;
的橫坐標的函數,利用函數的性質求最大值;
(3)分別以![]() 為邊與對角線進行討論,利用矩形的性質與拋物線的性質及平移的特點求解
為邊與對角線進行討論,利用矩形的性質與拋物線的性質及平移的特點求解![]() 的坐標,再利用函數知識或三角函數或相似建立方程即可得到答案.
的坐標,再利用函數知識或三角函數或相似建立方程即可得到答案.
解(1)令![]() ,得
,得![]() ,
,
因為:![]() ,所以
,所以![]() ,
,
所以:![]() ,
,
![]() ,
,![]() ,
,
拋物線的對稱軸是:直線![]() ;
;
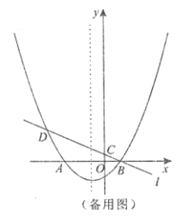
(2)過點![]() 作
作![]() 軸交直線
軸交直線![]() 于點
于點![]() ,如圖1,
,如圖1,
∵![]() ,∴拋物線的解析式為
,∴拋物線的解析式為![]() , 直線
, 直線![]() 的解析式為
的解析式為![]()
設點![]() ,則
,則![]()
∴![]()
![]()
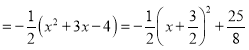
∵![]() ,∴當
,∴當![]() 時,
時,![]() 面積的最大值為
面積的最大值為![]() .
.
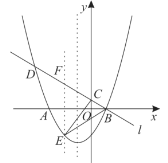
圖1
(3)聯立: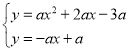 ,得
,得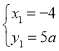 ,
,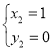
∴點![]()
①若點![]() 、
、![]() 、
、![]() 、
、![]() 為頂點的矩形中
為頂點的矩形中![]() ,
,
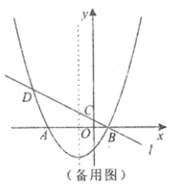
過點![]() 作
作![]() 軸,過點
軸,過點![]() 作
作![]() 于點
于點![]() 如圖2,
如圖2,
則![]() ,
,![]() ,
,![]() ,
,
∴![]() ,則點
,則點![]() 的坐標為
的坐標為![]() ,
,
由平移得,點![]() 的坐標為
的坐標為![]() ,
,
∴![]() ,
,
∴![]() ,∴
,∴![]() (負值合去)
(負值合去)
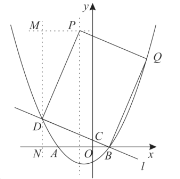
圖2
②若矩形![]() 中
中![]() 為對角線,∵
為對角線,∵![]() ,
,![]() ,
,
由![]() ,
,
則由平移可得:點![]() 的坐標為
的坐標為![]() ,
,
過點![]() 作
作![]() 軸,點
軸,點![]() 作
作![]() 軸,
軸,
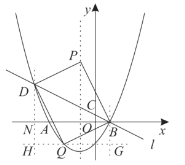
過點![]() 作
作![]() 于點
于點![]() ,交
,交![]() 于點
于點![]() ,如圖3,
,如圖3,
則![]() ,
,
![]() ,
,![]() ,
,
∴![]() ,∴
,∴![]() (負值舍去)
(負值舍去)
∴當點![]() 、
、![]() 、
、![]() 、
、![]() 為頂點的四邊形為矩形時,
為頂點的四邊形為矩形時,![]() 的值為
的值為![]() ,
,![]() .
.


科目:初中數學 來源: 題型:
【題目】如圖,二次函數y=ax2+2ax+c(a<0)的圖象與x軸交于A、B兩點,與y軸交于C點,頂點為D,一次函數y=mx﹣3的圖象與y軸交于E點,與二次函數的對稱軸交于F點,且tan∠FDC=![]() .
.
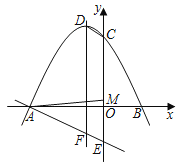
(1)求a的值;
(2)若四邊形DCEF為平行四邊形,求二次函數表達式.
(3)在(2)的條件下設點M是線段OC上一點,連接AM,點P從點A出發,先以1個單位長度/s的速度沿線段AM到達點M,再以![]() 個單位長度/s的速度沿MC到達點C,求點P到達點C所用最短時間為 s(直接寫出答案).
個單位長度/s的速度沿MC到達點C,求點P到達點C所用最短時間為 s(直接寫出答案).
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在等腰![]() 中,
中,![]() 點
點![]() 為直線
為直線![]() 上一動點(點
上一動點(點![]() 不與
不與![]() 、
、![]() 重合).以
重合).以![]() 為邊向右側作正方形
為邊向右側作正方形![]() ,連結
,連結![]() .
.
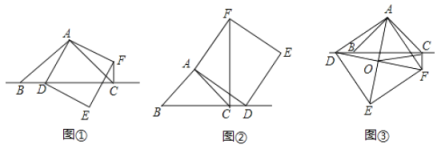
(猜想)如圖①,當點![]() 在線段
在線段![]() 上時,直接寫出
上時,直接寫出![]() 、
、![]() 、
、![]() 三條線段的數量關系.
三條線段的數量關系.
(探究)如圖②,當點![]() 在線段
在線段![]() 的延長線上時,判斷
的延長線上時,判斷![]() 、
、![]() 、
、![]() 三條線段的數量關系,并說明理由.
三條線段的數量關系,并說明理由.
(應用)如圖③,當點![]() 在線段
在線段![]() 的反向延長線上時,點
的反向延長線上時,點![]() 、
、![]() 分別在直線
分別在直線![]() 兩側,
兩側,![]() 、
、![]() 交點為點
交點為點![]() 連結
連結![]() ,若
,若![]() ,
,![]() ,則
,則![]() .
.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】學習一定要講究方法,比如有效的預習可大幅提高聽課效率.九年級(1)班學習興趣小組為了了解全校九年級學生的預習情況,對該校九年級學生每天的課前預習時間(單位:![]() )進行了抽樣調查.并將抽查得到的數據分成5組,下面是未完成的頻數、頓率分布表和頻數分布扇形圖.
)進行了抽樣調查.并將抽查得到的數據分成5組,下面是未完成的頻數、頓率分布表和頻數分布扇形圖.
組別 | 課前預習時間 | 頻數(人數) | 頻率 |
1 |
| 2 | |
2 |
|
| 0.10 |
3 |
| 16 | 0.32 |
4 |
|
|
|
5 |
| 3 |
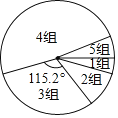
請根據圖表中的信息,回答下列問題:
(1)本次調查的樣本容量為 ,表中的![]() ,
,![]() ,
,![]() ;
;
(2)試計算第4組人數所對應的扇形圓心角的度數;
(3)該校九年級其有1000名學生,請估計這些學生中每天課前預習時間不少于![]() 的學生人數.
的學生人數.
查看答案和解析>>
科目:初中數學 來源: 題型:
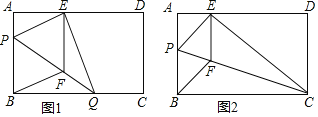
【題目】如圖1,在矩形紙片ABCD中,AB=12cm,AD=20cm,折疊紙片使B點落在邊AD上的E處,折痕為PQ,過點E作EF∥AB交PQ于F,連接BF.
(1)求證:四邊形BFEP為菱形;
(2)當點E在AD邊上移動時,折痕的端點P、Q也隨之移動;
①當點Q與點C重合時(如圖2),求菱形BFEP的邊長;
②若限定P、Q分別在邊BA、BC上移動,求出點E在邊AD上移動的最大距離.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,點![]() 在直線
在直線![]() 上,過點
上,過點![]() 作
作![]() ,且
,且![]() ,點
,點![]() 在射線
在射線![]() 上(點
上(點![]() 不與點
不與點![]() 重合),且滿足
重合),且滿足![]() ,
,![]() ,
,![]() 與
與![]() 交于點
交于點![]() ,過點
,過點![]() 作
作![]() 于點
于點![]() .設
.設![]()
![]() .
.
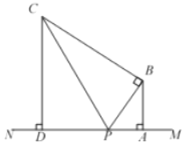
(1)用含![]() 的代數式表示
的代數式表示![]() 的長;
的長;
(2)①線段![]() 的長是________;
的長是________;
②線段![]() 的長是_________;(用含
的長是_________;(用含![]() 的代數式表示)
的代數式表示)
(3)當![]() 為何值時,
為何值時,![]() 有最小值?并求出這個最小值.
有最小值?并求出這個最小值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某商場以每件10元的價格購進一種商品,試銷中發現,這種商品每天的銷售量m(件)與每件的銷售價x(元)滿足一次函數,其函數圖像如圖所示.

(1)求商場每天銷售這種商品的銷售利潤y(元)與每件的銷售價x(元)之間的函數解析式;
(2)試判斷,每件商品的銷售價格在什么范圍內,每天的銷售利潤隨著價格的提高而增加.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com