
【題目】問題背景:在![]() 中,
中,![]() 邊上的動點
邊上的動點![]() 由
由![]() 向
向![]() 運動(與
運動(與![]() ,
,![]() 不重合),點
不重合),點![]() 與點
與點![]() 同時出發(fā),由點
同時出發(fā),由點![]() 沿
沿![]() 的延長線方向運動(
的延長線方向運動(![]() 不與
不與![]() 重合),連結(jié)
重合),連結(jié)![]() 交
交![]() 于點
于點![]() ,點
,點![]() 是線段
是線段![]() 上一點.
上一點.
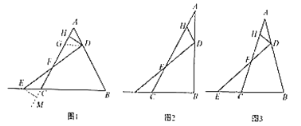
(1)初步嘗試:如圖,若![]() 是等邊三角形,
是等邊三角形,![]() ,且點
,且點![]() ,
,![]() 的運動速度相等,求證:
的運動速度相等,求證:![]() .
.
小王同學(xué)發(fā)現(xiàn)可以由以下兩種思路解決此問題:
思路一:過點![]() 作
作![]() ,交
,交![]() 于點
于點![]() ,先證
,先證![]() ,再證
,再證![]() ,從而證得結(jié)論成立;
,從而證得結(jié)論成立;
思路二:過點![]() 作
作![]() ,交
,交![]() 的延長線于點
的延長線于點![]() ,先證
,先證![]() ,再證
,再證![]() ,從而證得結(jié)論成立.
,從而證得結(jié)論成立.
請你任選一種思路,完整地書寫本小題的證明過程(如用兩種方法作答,則以第一種方法評分)
(2)類比探究:如圖,若在![]() 中,
中,![]() ,
,![]() ,且點
,且點![]() ,
,![]() 的運動速度之比是
的運動速度之比是![]() ,求
,求![]() 的值;
的值;
(3)延伸拓展:如圖,若在![]() 中,
中,![]() ,
,![]() ,記
,記![]() ,且點
,且點![]() 、
、![]() 的運動速度相等,試用含
的運動速度相等,試用含![]() 的代數(shù)式表示
的代數(shù)式表示![]() (直接寫出結(jié)果,不必寫解答過程).
(直接寫出結(jié)果,不必寫解答過程).
【答案】(1)證明見解析;(2)![]() ;(3)
;(3)![]() .
.
【解析】
(1)過點D作DG∥BC,交AC于點G,先證明△ADG是等邊三角形,得出GD=AD=CE,再證明GH=AH,由ASA證明△GDF≌△CEF,得出GF=CF,即可得出結(jié)論;
(2)過點D作DG∥BC,交AC于點G,先證出AH=GH=GD,AD=![]() GD,由題意AD=
GD,由題意AD=![]() CE,得出GD=CE,再證明△GDF≌△CEF,得出GF=CF,即可得出結(jié)論;
CE,得出GD=CE,再證明△GDF≌△CEF,得出GF=CF,即可得出結(jié)論;
(3)過點D作DG∥BC,交AC于點G,先證出DG=DH=AH,再證明△ADG∽△ABC,△ADG∽△DGH,△DGH∽△ABC,得出![]() ,△DGH∽△ABC,得出
,△DGH∽△ABC,得出![]() ,證明△DFG∽△EFC,得出
,證明△DFG∽△EFC,得出![]() ,
,![]() ,即可得出結(jié)果.
,即可得出結(jié)果.
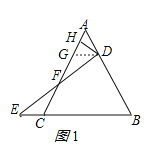
解:(1)證明:選擇思路一:
如題圖1,過點![]() 作
作![]() ,交
,交![]() 于點
于點![]() ,
,
∵![]() 是等邊三角形,∴
是等邊三角形,∴![]() ,
,![]() .
.
∴![]() 是等邊三角形.∴
是等邊三角形.∴![]() .
.
∵![]() ,∴
,∴![]() .
.
∵![]() ,∴
,∴![]() ,
,![]() .
.
∴![]() .∴
.∴![]() .
.
∴![]() ,即
,即![]() .
.
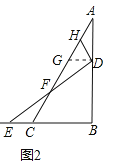
(2)如圖2,過點![]() 作
作![]() ,交
,交![]() 于點
于點![]() ,
,
則![]() ,
,
∵![]() ,∴
,∴![]() .
.
∴![]() ,
,![]() .
.
由題意可知,![]() ,∴
,∴![]() .
.
∵![]() ,∴
,∴![]() ,
,![]() .
.
∴![]() .∴
.∴![]() .
.
∴![]() ,即
,即![]() .
.
∴![]() .
.
(3)![]() ,理由如下:
,理由如下:
過點D作DG∥BC,交AC于點G,如圖3所示:
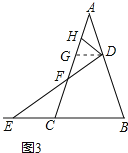
則∠ADG=∠B,∠AGD=∠ACB,
∵AB=AC,∠BAC=36°,
∴∠ACB=∠B=∠ADG=∠AGD=72°,
∵∠ADH=∠BAC=36°,
∴AH=DH,∠DHG=72°=∠AGD,
∴DG=DH=AH,△ADG∽△ABC,△ADG∽△DGH,
![]() ,
,
∴△DGH∽△ABC,
![]() ,
,
![]() ,
,
∵DG∥BC,
∴△DFG∽△EFC,
![]() ,
,
![]() ,
,
即![]() ,
,
![]() ,
,
![]() .
.


科目:初中數(shù)學(xué) 來源: 題型:
【題目】為保障我國海外維和部隊官兵的生活,現(xiàn)需通過A港口、B港口分別運送100噸和50噸生活物資.已知該物資在甲倉庫存有80噸,乙倉庫存有70噸,若從甲、乙兩倉庫運送物資到港口A的費用分別為14元/噸,20元/噸;從甲、乙兩倉庫運送物資到港口B的費用分別為10元/噸、8元/噸.
(Ⅰ)設(shè)從甲倉庫運往A港口x噸,試填寫表格.
表一
港口 | 從甲倉庫運(噸) | 從乙倉庫運(噸) |
A港 |
|
|
B港 |
|
|
表二
港口 | 從甲倉庫運到港口費用(元) | 從乙倉庫運到港口費用(元) |
A港 | 14x |
|
B港 |
|
|
(Ⅱ)給出能完成此次運輸任務(wù)的最節(jié)省費用的調(diào)配方案,并說明理由.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
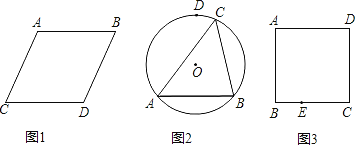
【題目】用無刻度直尺作圖(輔助線請畫虛線)
(1)如圖1,在ABCD中畫一條直線平分周長;
(2)如圖2,在⊙O中,AB為⊙O內(nèi)的一條弦,D為優(yōu)弧AB的中點,C為優(yōu)弧AB的一動點,畫出∠ACB的平分線;
(3)如圖3,在正方形ABCD中,E為CB上的任意一點,在AB上截取一點F,使得BF=BE.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,點A,B在反比例函數(shù)y=![]() (x>0)的圖象上,點C,D在反比例函數(shù)y=
(x>0)的圖象上,點C,D在反比例函數(shù)y=![]() (k>0)的圖象上,AC∥BD∥y軸,已知點A,B的橫坐標(biāo)分別為1,2,△OAC與△ABD的面積之和為
(k>0)的圖象上,AC∥BD∥y軸,已知點A,B的橫坐標(biāo)分別為1,2,△OAC與△ABD的面積之和為![]() ,則k的值為_____.
,則k的值為_____.

查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】在平面直角坐標(biāo)系xOy中,已知第一象限內(nèi)的點A在反比例函數(shù)y=![]() 的圖象上,第二象限內(nèi)的點B在反比例函數(shù)y=
的圖象上,第二象限內(nèi)的點B在反比例函數(shù)y=![]() 的圖象上,連接OA、OB,若OA⊥OB,OB=OA,則k=_____.
的圖象上,連接OA、OB,若OA⊥OB,OB=OA,則k=_____.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
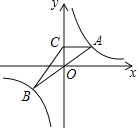
【題目】如圖,一直線經(jīng)過原點O,且與反比例函數(shù)y=![]() (k>0)相交于點A、點B,過點A作AC⊥y軸,垂足為C,連接BC.若△ABC面積為8,則k=_____.
(k>0)相交于點A、點B,過點A作AC⊥y軸,垂足為C,連接BC.若△ABC面積為8,則k=_____.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】小雨利用幾何畫板探究函數(shù)y=![]() 圖象,在他輸入一組a,b,c的值之后,得到了如圖所示的函數(shù)圖象,根據(jù)學(xué)習(xí)函數(shù)的經(jīng)驗,可以判斷,小雨輸入的參數(shù)值滿足( )
圖象,在他輸入一組a,b,c的值之后,得到了如圖所示的函數(shù)圖象,根據(jù)學(xué)習(xí)函數(shù)的經(jīng)驗,可以判斷,小雨輸入的參數(shù)值滿足( )
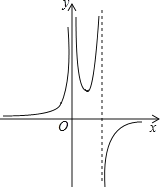
A.a>0,b>0,c=0B.a<0,b>0,c=0
C.a>0,b=0,c=0D.a<0,b=0,c>0
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
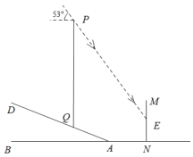
【題目】重慶移動為了提升新型冠狀肺炎“停課不停學(xué)”期間某片區(qū)網(wǎng)絡(luò)信號,保證廣大師生網(wǎng)絡(luò)授課、聽課的質(zhì)量,臨時在坡度為![]() 的山坡上加裝了信號塔
的山坡上加裝了信號塔![]() (如圖所示),信號塔底端
(如圖所示),信號塔底端![]() 到坡底
到坡底![]() 的距離為3.9米.同時為了提醒市民,在距離斜坡底4.4米的水平地面上立了一塊警示牌
的距離為3.9米.同時為了提醒市民,在距離斜坡底4.4米的水平地面上立了一塊警示牌![]() .當(dāng)太陽光線與水平線成53°角時,測得信號塔
.當(dāng)太陽光線與水平線成53°角時,測得信號塔![]() 落在警示牌上的影子
落在警示牌上的影子![]() 長為3米,則信號塔
長為3米,則信號塔![]() 的高約為(tan53°≈1.3)( ).
的高約為(tan53°≈1.3)( ).
A.10.4B.11.9C.11.4D.13.4
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com