
【題目】如圖,在平面直角坐標系中,拋物線![]() 與x軸交于A,B兩點(點A在點B左側),與y軸交于點C.
與x軸交于A,B兩點(點A在點B左側),與y軸交于點C.
(1)判斷ABC的形狀,并說明理由;
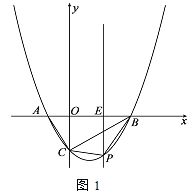
(2)如圖1,點P為直線BC下方的二次函數圖象上的一個動點(點P與B、C不重合),過點P作y軸的平行線交x軸于點E.當PBC面積的最大值時,點F為線段BC一點(不與點、重合),連接EF,動點G從點E出發,沿線段EF以每秒1個單位的速度運動到點F,再沿FC以每秒![]() 個單位的速度運動到點C后停止,當點F的坐標是多少時,點G在整個運動過程中用時最少?
個單位的速度運動到點C后停止,當點F的坐標是多少時,點G在整個運動過程中用時最少?
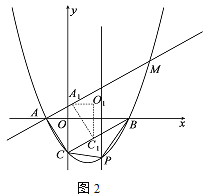
(3)如圖2,將ACO沿射線CB方向以每秒![]() 個單位的速度平移,記平移后的ACO為A1C1O1,連接A A1,直線A A1交拋物線與點M,設平移的時間為t秒,當A MC1為等腰三角形時,求t的值.
個單位的速度平移,記平移后的ACO為A1C1O1,連接A A1,直線A A1交拋物線與點M,設平移的時間為t秒,當A MC1為等腰三角形時,求t的值.
【答案】(1)△ABC為直角三角形,理由見解析;(2)![]() ;(3)當△AMC1為等腰三角形時,則t的值t=
;(3)當△AMC1為等腰三角形時,則t的值t=![]() 或
或![]() 或
或![]() 或
或![]() .
.
【解析】(1)結論:△ABC是直角三角形.在Rt△AOC中,由tan∠ACO=![]() ,推出∠ACO=30°,在Rt△OBC中,由tan∠BCO=
,推出∠ACO=30°,在Rt△OBC中,由tan∠BCO=![]() ,推出∠BCO=60°,可得∠ACB=∠ACO+∠BCO=90°;
,推出∠BCO=60°,可得∠ACB=∠ACO+∠BCO=90°;
(2)設P(m,![]() m2-
m2-![]() m-
m-![]() ),作射線CN,使得∠BCN=60°,作FH⊥CN于H,FG⊥AE于G,則FH=CFcos30°=
),作射線CN,使得∠BCN=60°,作FH⊥CN于H,FG⊥AE于G,則FH=CFcos30°=![]() CF,首先求出點P坐標,動點G的運動時間=
CF,首先求出點P坐標,動點G的運動時間=![]() CF=EF+FH,根據垂線段最短可知,當EH⊥CN時,動點G的運動時間最小,由此即可解決問題;
CF=EF+FH,根據垂線段最短可知,當EH⊥CN時,動點G的運動時間最小,由此即可解決問題;
(3)求出直線AM的解析式,利用方程組求出點M坐標,由題意C′(t,![]() t-
t-![]() ),分三種情形討論,想辦法列出方程即可解決問題;
),分三種情形討論,想辦法列出方程即可解決問題;
(1)結論:△ABC是直角三角形.
理由:如圖1中,連接AC.
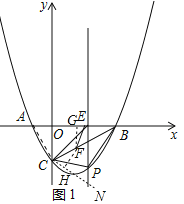
∵拋物線y=![]() x2-
x2-![]() x-
x-![]() 與x軸交于A、B兩點(點A在點B左側),與y軸交于點C,
與x軸交于A、B兩點(點A在點B左側),與y軸交于點C,
∴A(-1,0),B(3,0),C(0,-![]() ),
),
在Rt△AOC中,∵tan∠ACO=![]() ,
,
∴∠ACO=30°,
在Rt△OBC中,∵tan∠BCO=![]() ,
,
∴∠BCO=60°,
∴∠ACB=∠ACO+∠BCO=90°,
∴△ABC是直角三角形.
(2)設P(m,![]() m2-
m2-![]() m-
m-![]() ),作射線CN,使得∠BCN=60°,作FH⊥CN于H,FG⊥AE于G,則FH=CFcos30°=
),作射線CN,使得∠BCN=60°,作FH⊥CN于H,FG⊥AE于G,則FH=CFcos30°=![]() CF.
CF.
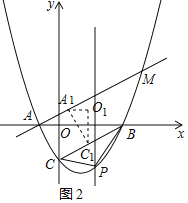
則S△PBC=S△POC+S△POB-S△BOC
=![]() ×
×![]() ×m+
×m+![]() ×3×(-
×3×(-![]() m2+
m2+![]() m+
m+![]() )-
)-![]() ×
×![]() ×3
×3
=-![]() (m-
(m-![]() )2+
)2+ ![]() ,
,
∵-![]() <0,
<0,
∴m=![]() 時,△PBC的面積最大,此時P(
時,△PBC的面積最大,此時P(![]() ,-
,-![]() ),
),
∵動點G的運動時間=![]() CF=EF+FH,
CF=EF+FH,
根據垂線段最短可知,當EH⊥CN時,動點G的運動時間最小,
∵∠EFB=∠EBF=30°,
∴EF=EB=![]() ,
,
在Rt△EFG中,FG=EFcos30°=![]() ,EG=
,EG=![]() ,OG=
,OG=![]() ,
,
∴此時F的坐標為(![]() ,-
,-![]() ).
).
(3)由題意直線BC的解析式為y=![]() x-
x-![]() ,直線AC的解析式為y=
,直線AC的解析式為y=![]() x+
x+![]() ,
,
由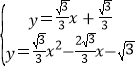 ,
,
解得![]() ,或
,或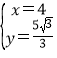
∴M(4,![]() ),
),
∵C1(t,![]() t-
t-![]() ),
),
∴AM2=52+(![]() )2,C1A2=(t+1)2+(
)2,C1A2=(t+1)2+(![]() t-
t-![]() )2,MC1=(4-t)2+(
)2,MC1=(4-t)2+(![]() -
-![]() t+
t+![]() )2,
)2,
①當AM=MC1時,52+(![]() )2=(4-t)2+(
)2=(4-t)2+(![]() -
-![]() t+
t+![]() )2,解得t=5+
)2,解得t=5+![]() 或5-
或5-![]() ,
,
②當C1A=C1M時,(t+1)2+(![]() t-
t-![]() )2=(4-t)2+(
)2=(4-t)2+(![]() -
-![]() t+
t+![]() )2,解得t=
)2,解得t=![]()
③當C1A=AM時,52+(![]() )2=(t+1)2+(
)2=(t+1)2+(![]() t-
t-![]() )2,解得t=
)2,解得t=![]() s或-
s或-![]() (舍棄),
(舍棄),
綜上所述,滿足條件的t的值為(5+![]() )s或(5-
)s或(5-![]() )s或
)s或![]() s或
s或![]() s.
s.


 閱讀快車系列答案
閱讀快車系列答案科目:初中數學 來源: 題型:
【題目】根據閱讀材料,回答問題.
材料:如圖所示,有公共端點(O)的兩條射線組成的圖形叫做角(![]() ).如果一條射線(
).如果一條射線(![]() )把一個角(
)把一個角(![]() )分成兩個相等的角(
)分成兩個相等的角(![]() 和
和![]() ),這條射線(
),這條射線(![]() )叫做這個角的平分線.這時,
)叫做這個角的平分線.這時,![]() (或
(或![]() ).
).
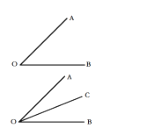
問題:平面內一定點A在直線![]() 的上方,點O為直線
的上方,點O為直線![]() 上一動點,作射線
上一動點,作射線![]() ,
,![]() ,
,![]() ,當點O在直線
,當點O在直線![]() 上運動時,始終保持
上運動時,始終保持![]() ,
,![]() ,將射線
,將射線![]() 繞點O順時針旋轉60°得到射線
繞點O順時針旋轉60°得到射線![]() .
.
(1)如圖1,當點O運動到使點A在射線![]() 的左側時,若
的左側時,若![]() 平分
平分![]() ,求
,求![]() 的度數;
的度數;
(2)當點O運動到使點A在射線![]() 的左側,
的左側,![]() 時,求
時,求![]() 的值;
的值;
(3)當點O運動到某一時刻時,![]() ,直接寫出此時
,直接寫出此時![]() 的度數.
的度數.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,平面上有射線![]() 和點
和點![]() ,
,![]() ,請用尺規按下列要求作圖:
,請用尺規按下列要求作圖:
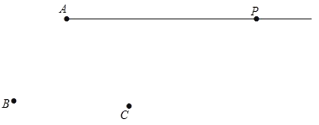
(1)連接![]() ,并在射線
,并在射線![]() 上截取
上截取![]() ;
;
(2)連接![]() 、
、![]() ,并延長
,并延長![]() 到
到![]() ,使
,使![]()
(3)在(2)的基礎上,取![]() 中點
中點![]() ,若
,若![]() ,
,![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系中,直線AB與x軸交于點B,與y軸交于點A,與反比例函數![]() 的圖象在第二象限交于點C,CE⊥x軸,垂足為點E,
的圖象在第二象限交于點C,CE⊥x軸,垂足為點E,![]() ,OB=2,OE=1.
,OB=2,OE=1.
(1)求反比例函數的解析式;
(2)若點D是反比例函數圖象在第四象限上的點,過點D作DF⊥y軸,垂足為點F,連接OD、BF,如果SBAF=4SDFO,求點D的坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】為了了解市民“獲取新聞的最主要途徑”,某市記者開展了一次抽樣調查,根據調查結果繪制了如下尚不完整的統計圖.
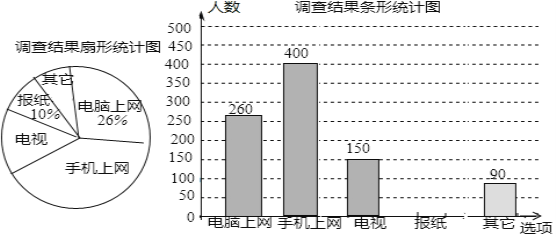
根據以上信息解答下列問題.
(1)這次抽樣調查的樣本容量是__________.
(2)通過“電視”了解新聞的人數占被調查人數的百分比為______;扇形統計圖中,“手機上網”所對應的圓心角的度數是_________.
(3)請補全條形統計圖;
(4)若該市約有950萬人,請你估計其中將“電腦和手機上網”作為“獲取新聞的最主要途徑”的總人數.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某校組織學生開展課外社會實踐活動,現有甲、乙兩種大客車可租,已知1輛甲種客車和3輛乙種客車共需租金1240元,3輛甲種客車和2輛乙種客車共需租金1760元.
(1)求1輛甲種客車和1輛乙種客車的租金分別是多少元?
(2)學校計劃租用甲、乙兩種客車共8輛,甲種客車每輛載客量45人,乙種客車每輛載客量30人,共有師生330人,求最節省的租車費用是多少元?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,點B,E,C,F在同一條直線上,AB=DE,∠B=∠DEF.要使△ABC≌△DEF,則需要再添加的一個條件是_______.(寫出一個即可)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】“水是生命之源”,某市自來水公司為了鼓勵居民節約用水,規定按以下標準收取水費:
月用水量(噸) | 單價(元/噸) |
不超過25噸 | 1.4 |
超過25噸的部分 | 2.1 |
另:每噸用水加收0.95元的城市污水處理費 | |
(1)如果1月份小明家用水量為18噸,那么小明家1月份應該繳納水費 元;
(2)小明家2月份共繳納水費104.5元,那么小明家2月份用水多少噸?
(3)小明家的水表3月份出了故障,只有80%的用水量記入水表中,這樣小明家在3月份只繳納了56.4元水費,問小明家3月份實際應該繳納水費多少元?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com