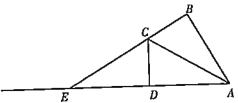
【題目】如圖，在四邊形
中，
是對角線，
，
，延長
交
的延長線于點
.
（1）求證：
；
（2）若
，求
的值；
（3）過點作
，交的延長線于點
，過點作
，交
的延長線于點
，連接
.設
，點
是直線
上的動點，當
的值最小時，點與點是否可能重合？若可能，請說明理由并求此時的值（用含
的式子表示）；若不可能，請說明理由.
【答案】（1）見解析；（2）
；（3）可以重合，理由見解析，
的最小值為
.
【解析】
（1）運用HL證明
即可得到結論；
（2）根據已知條件可證出AB=BE，從而可得∠BAE=45°,再由角平分線的定義可得∠BAC的度數；
（3）連接
，連接
，延長
交
的延長線于點
.證明點
與點關于直線
成軸對稱，也即點
、點
、點關于直線的對稱點，這三點共線，也即的值最小時，點
與點重合.再證明
為等邊三角形即可得到結論.
（1）證明：
，
，
，
.
.
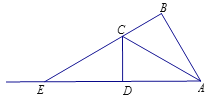
（2）
，
又
，
.
，
.
.
，
.
由（1）得
，
.
.
（3）當
的值最小時，點與點可以重合，理由如下：
，
，
.
，
.
.
.
由（1）得，，
，
.即
平分
.
又
，
，
.
連接，連接，延長交的延長線于點.
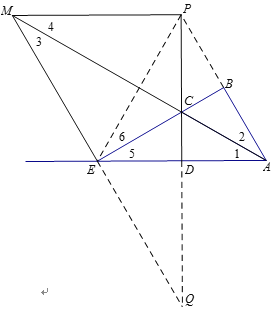
設
，則
.
在
中，
.
在
中，
.
，
.
，
.
當
時，
，
，
.
.
即點
與點關于直線成軸對稱，也即點、點、點關于直線的對稱點，這三點共線，也即的值最小時，點與點重合.
因為當時，
，也即
.
所以，當
時，取最小值時的點與點重合.
此時的最小值即為
.
，
，
，
.
.
.
，
，三點共線.
當時，在
中，
.
∴ ∠EPA＝60°.
為等邊三角形
.
，
.
.
，
.
的最小值為.
名校課堂系列答案科目：初中數學 來源： 題型：
【題目】如圖，一艘輪船位于燈塔P的北偏東60°方向，與燈塔P的距離為80海里的A處，它沿正南方向航行一段時間后，到達位于燈塔P的南偏東45°方向的B處，求此時輪船所在的B處與燈塔P的距離．（參考數據：
≈2.449，結果保留整數）
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】已知二次函數y=ax2+bx+c（a≠0）的圖象如圖，在下列代數式中（1）a+b+c＞0；（2）﹣4a＜b＜﹣2a（3）abc＞0；（4）5a﹣b+2c＜0； 其中正確的個數為（ ）
A. 1個 B. 2個 C. 3個 D. 4個
查看答案和解析>>
科目：初中數學 來源： 題型：
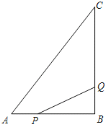
【題目】如圖所示，
中，
，
，
．
點
從點
開始沿
邊向
以
的速度移動，點
從點開始沿
邊向點
以
的速度移動．如果、分別從，同時出發，線段
能否將分成面積相等的兩部分？若能，求出運動時間；若不能說明理由．
若點沿射線方向從點出發以的速度移動，點沿射線
方向從點出發以的速度移動，、同時出發，問幾秒后，
的面積為
？
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】我們定義：如果一個三角形一條邊上的高等于這條邊，那么這個三角形叫做“等高底”三角形，這條邊叫做這個三角形的“等底”．
（1）概念理解：
如圖1，在△ABC中，AC=6，BC=3，∠ACB=30°，試判斷△ABC是否是”等高底”三角形，請說明理由．
（2）問題探究：
如圖2，△ABC是“等高底”三角形，BC是”等底”，作△ABC關于BC所在直線的對稱圖形得到△A'BC，連結AA′交直線BC于點D．若點B是△AA′C的重心，求
的值．
（3）應用拓展：
如圖3，已知l1∥l2，l1與l2之間的距離為2．“等高底”△ABC的“等底”BC在直線l1上，點A在直線l2上，有一邊的長是BC的
倍．將△ABC繞點C按順時針方向旋轉45°得到△A'B'C，A′C所在直線交l2于點D．求CD的值．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖①，四邊形OACB為長方形，A（﹣6，0），B（0，4），直線l為函數y＝﹣2x﹣5的圖象．
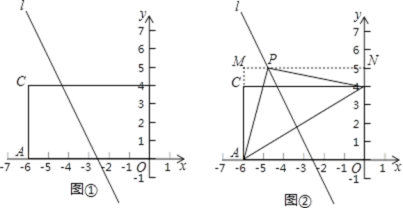
（1）點C的坐標為 ；
（2）若點P在直線l上，△APB為等腰直角三角形，∠APB＝90°，求點P的坐標；
小明的思考過程如下：
第一步：添加輔助線，如圖②，過點P作MN∥x軸，與y軸交于點N，與AC的延長線交于點M；
第二步：證明△MPA≌△NBP；
第三步：設NB＝m，列出關于m的方程，進而求得點P的坐標．
請你根據小明的思考過程，寫出第二步和第三步的完整解答過程；
（3）若點P在直線l上，點Q在線段AC上（不與點A重合），△QPB為等腰直角三角形，直接寫出點P的坐標．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，在△ABC中，∠BAC=90°，AD是高，BE是中線，CF是角平分線，CF交AD于點G，交BE于點H，下面說法中正確的序號是_____．
①△ABE的面積等于△BCE的面積；②∠AFG=∠AGF；③∠FAG=2∠ACF；④BH=CH．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】（模型建立）
（1）如圖1，等腰直角三角形ABC中，∠ACB＝90°，CB＝CA，直線ED經過點C，過A作AD⊥ED于點D，過B作BE⊥ED于點E．
求證：△BEC≌△CDA；
（模型應用）
（2）① 已知直線l1：y＝
x＋8與坐標軸交于點A、B，將直線l1繞點A逆時針旋轉45
至直線l2，如圖2，求直線l2的函數表達式；
② 如圖3，長方形ABCO，O為坐標原點，點B的坐標為（8，－6），點A、C分別在坐標軸上，點P是線段BC上的動點，點D是直線y＝－3x＋6上的動點且在y軸的右側．若△APD是以點D為直角頂點的等腰直角三角形，請直接寫出點D的坐標．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，∠AOB=60°，OA=OB，動點C從點O出發，沿射線OB方向移動，以AC為邊在右側作等邊△ACD，連接BD，則BD所在直線與OA所在直線的位置關系是（ ）
A. 平行 B. 相交 C. 垂直 D. 平行、相交或垂直
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com