科目：初中數學 來源： 題型：
下列是由四個相同小正方體擺成的立方體圖形，它的俯視圖是（ ）
| A． B． C． D． |
1． 我州今年參加中考的學生人數大約為
人，對于這個科學記數法表示的近似數，下列說法正確的是（ ）
A．精確到百分位，有3個有效數字 B．精確到百分位，有5個有效數字
C．精確到百位，有3個有效數字 D．精確到百位，有5個有效數字
2． 
如圖，將一塊三角板的執教頂點放在直尺的一邊上，當
時，
（ ）
A．
B．
C．
D．
3． 下列根式中，不能與
合并的是（ ）
A．
B．
C．
D．
某班45名同學某天每人的生活費用統計如下表：
| 生活費（元） | 10 | 15 | 20 | 25 | 30 |
| 學生人數（人） | 4 | 10 | 15 | 10 | 6 |
對于這45名同學這天每人的生活費用，下列說法不正確的是（ ）A．平均數是20 B．眾數 C．中位數是20 D．極差是2021世紀教育網版權所有
4． 關于
的一元二次方程
有實數根，則
的取值范圍是（ ）
A．
B．
C．且
D．且
5． 將圓心角為
，面積為
的扇形圍成一個圓錐的側面，則所圍成圓錐的底面半徑為（ ）
A．
B．
C．
D．
6． 在平面直角坐標系中，點
（
，2）關于直線
對稱點的坐標是（ ）
A．（，
） B．（3，2） C．（2，） D．（3，）
7． 如圖，
內接于
，
，則
的度數為（ ）
A．
B．
C．
D．
8． 以正方形
兩條對角線的交點
為坐標原點，建立如圖所示的平面直角坐標系，雙曲線
經過點
，則正方形的面積是（ ）21·cn·jy·com
A．10 B．11 C．12 D．13
9． 二次函數
（
）的圖象如圖所示，下列說法：①
；②當
時，
；③若點（
，
）和點（
，
）都在函數的圖象上，當
時，
；④
。其中正確的是（ ）21·世紀*教育網
A．① ② ④ B．① ④ C．① ② ③ D．③ ④
第II卷（選擇題 共72分）
二、填空題：（共5個小題，每小題4分，共20分）
10．
的平方根是 。
11．已知函數
是正比例函數，則
，
。
12．
小明同學根據全班同學的血型繪制了如圖所示的扇形統計圖，已知
型血的有20人，則型血的有 人。21教育網
13．分式方程
的解是 。
14．在
中，
、
是
邊上的三等分點，連接
、
相交于點，則
。2-1-c-n-j-y
三、解答題：（共2小題，每小題6分，共12分）
15．計算：
；
16．先化簡：
，然后從
的范圍內選取一個合適的整數作為的值代入求值。
四、解答題：（共3小題，每小題8分，共24分）
17．如圖，在樓房
和塔
之間有一棵樹
，從樓頂處經過樹頂
點恰好看到塔的底部點，且俯角
為
，從樓底
點1米的點處經過樹頂點恰好看到塔的頂部
點，且仰角
為
。已知樹高
米，求塔的高度（結果保留根號）。
18．如圖，在正方形中，
是
上任意一點，連接
，
于，
交于
，探究線段
、
、三者之間的數量關系，并說明理由。
19．2015年5月6日，涼山州政府在邛海“空列”項目考察座談會上與多方達成初步合作意向，決定共同出資60.8億元，建設40千米的環邛海空中列車，這將是國內第一條空中列車。據計算，將有24千米的“空列”軌道假設在水上，其余假設在陸地上，并且每千米水上建設費用比陸地建設費用多0.2億元。 21*cnjy*com
（1）求每千米 “空列”軌道的水上建設費用和陸地建設費用各需多少億元？
（2）設計在某段“空列”軌道的建設中，每天至少需要運送沙石
，施工方準備租用大、小兩種運輸車共十輛。已知每輛大車每天運送沙石
，每輛小車每天運送沙石
，大、小車每天每輛租車費用分別是1000元，700元，且要求每天租車的總費用不得超過9300元，問施工方有幾種租車方案？那種租車方案費用最低，最低費用是多少？
五、解答題：（共2小題，每小題8分，共16分）
20．有甲、乙兩個不透明的布袋，甲袋中裝有3個完全相同的小球，分別標有數字0、1、2；乙袋中裝有3個完全相同的小球，分別標有數字
、、0；先從甲袋中隨機取出一個小球，記錄標有的數字為，再從乙袋中隨機取出一個小球，記錄標有的數字為
，確定點（，）。www.21-cn-jy.com
（1）用樹狀圖或列表法列舉點所有可能的坐標；
（2）求點（，）在函數
的圖象上的概率 ；
（3）在平面直角坐標系
中，的半徑是2，求過點（，）能作的切線的概率；
21．閱讀理解：
材料1：一組對邊平行，另一組對邊不平行的四邊形叫梯形。其中平行的兩邊叫做梯形的底邊，不平行的兩邊叫做梯形的腰。連接梯形兩腰中點的線段叫做梯形的中位線。
梯形的中位線具有下列性質：
梯形的中位線平行于兩底，并且等于兩底和的一半。
如圖（1），在梯形中，
。
∵、分別是、
的中點，
∴
，
。
材料2：經過三角形一邊的中點與另一邊平行的直線必平分第三邊。
如圖（2），在中，∵是的中點，
，
∴是
的中點。
請你運用所學知識，結合上述材料，解答下列問題：
如圖（3），在梯形中，，
于，、分別是、的中點，
。
（1）求證：
；
（2）若
，
，求
的長。
B卷（共30分）
二、填空題：（共2小題，每小題5分，共10分）
22．已知實數、
滿足
，
，則
。
23．菱形
在平面直角坐標系中的位置如圖所示，頂點（2，0），
，點是對角線
上一個動點， （0，），當
最短時，點的坐標為 。2·1·c·n·j·y
二、解答題：（共2小題，27題8分，28題12分，共20分）
24．如圖，的半徑為5，點在外，
交于、兩點，
交于、兩點。
（1）求證：
；（2）若
，
，
，求點到的距離。
25．如圖，已知拋物線
的頂點在軸的正半軸上，一次函數
與拋物線交于、兩點，與、軸分別交于、兩點。
（1）求的值；
（2）求、兩點的坐標；
（3）點（
，
）（
）是拋物線上一點，當
得面積是面積的2倍時，求、的值。
查看答案和解析>>
科目：初中數學 來源： 題型：
如圖，已知拋物線
的頂點
在
軸的正半軸上，一次函數
與拋物線交于
、
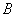兩點，與、
軸分別交于
、
兩點。
（1）求
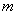的值；
（2）求、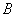兩點的坐標；
（3）點
（
，
）（
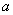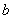）是拋物線上一點，當
得面積是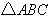
面積的2倍時，求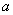、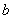的值。
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
的解是 。
時，
（ ）
B．
C．
D．
兩條對角線的交點
為坐標原點，建立如圖所示的平面直角坐標系，雙曲線
經過點
是
上任意一點，連接
，
于
交
，探究線段
、
、
三者之間的數量關系，并說明理由。
（
），且
，那么
=_____
∥
∥
，兩條直線與這三條平行線分別交于點
、
、
和
、
、
，已知
，
的值為
