
【題目】已知⊙O的半徑為5,EF是長為8的弦,OG⊥EF于點G,點A在GO的延長線上,且AO=13.弦EF從圖1的位置開始繞點O逆時針旋轉,在旋轉過程中始終保持OG⊥EF,如圖2.
[發現]在旋轉過程中,
(1)AG的最小值是 ,最大值是 .
(2)當EF∥AO時,旋轉角α= .
[探究]若EF繞點O逆時針旋轉120°,如圖3,求AG的長.
[拓展]如圖4,當AE切⊙O于點E,AG交EO于點C,GH⊥AE于H.
(1)求AE的長.
(2)此時EH= ,EC= .

【答案】發現:(1)10,16;(2)90°或270°;探究:AG=![]() ;拓展:(1)AE=12;(2)
;拓展:(1)AE=12;(2)![]() ,
,![]() .
.
【解析】
發現:(1)根據垂徑定理得:![]() 在Rt△EOG中,根據勾股定理求出OG=3,由旋轉知,點G的軌跡是以點O為圓心,OG=3為半徑的圓,即可求出AG的最大值與最小值.
在Rt△EOG中,根據勾股定理求出OG=3,由旋轉知,點G的軌跡是以點O為圓心,OG=3為半徑的圓,即可求出AG的最大值與最小值.
(2)根據OG⊥EF,EF∥OA,得出OG⊥OA,即可求出旋轉角度.
探究:過點G作GQ⊥OA于Q,在Rt△OQG中,求出∠GOQ的度數,根據含![]() 角的直角三角形的性質求出
角的直角三角形的性質求出![]() 即可求出AG的長
即可求出AG的長
拓展:(1)根據切線的性質得到∠OEA=90°,根據勾股定理即可求出AE的長.
(2)過點G作GP⊥OE于P,易證四邊形EHGP是矩形,證明△OGE∽△OPG,根據相似三角形的性質得到![]() 即可求出
即可求出![]() 的長度,即可求出EH的長度,再根據△AEC∽△AHG,求出EC的長度.
的長度,即可求出EH的長度,再根據△AEC∽△AHG,求出EC的長度.
發現:(1)如圖1,
連接OE,
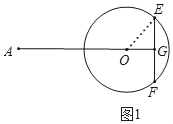
∵OG⊥EF,
∴![]()
在Rt△EOG中,OE=5,根據勾股定理得,OG=3,
由旋轉知,點G的軌跡是以點O為圓心,OG=3為半徑的圓,
∴AG最大=OA+OG=13+3=16,
AG最小=OA﹣OG=13﹣3=10,
故答案為:10,16;
(2)∵OG⊥EF,EF∥OA,
∴OG⊥OA,
∴旋轉角α=90°或270°,
故答案為90°或270°;
探究:如圖3,
過點G作GQ⊥OA于Q,
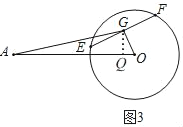
在Rt△OQG中,∠GOQ=180°﹣120°=60°,OG=3,
∴![]()
∴![]()
在Rt△AQG中, ![]()
拓展:(1)∵AE切⊙O于E,
∴∠OEA=90°,
在Rt△AEO中,![]()
(2)如圖4,
過點G作GP⊥OE于P,
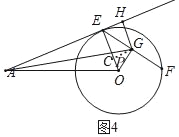
∵HG⊥AE,OE⊥AE,
∴四邊形EHGP是矩形,
∴HG=EP,EH=PG,
∵∠OGE=∠OPG=90°,∠GOE=∠POG,
∴△OGE∽△OPG,
∴![]()
∴![]()
∴![]()
∴![]()
![]()
∵OE⊥AE,HG⊥AE,
∴CE∥HG,
∴△AEC∽△AHG,
∴![]()
∴![]()
∴![]()
故答案為:![]()


 學業測評一課一測系列答案
學業測評一課一測系列答案科目:初中數學 來源: 題型:
【題目】(1)當![]() __________時,
__________時,![]() 有意義;(2)當
有意義;(2)當![]() __________時,
__________時,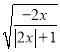 有意義;
有意義;
(3)當__________時,![]() 有意義;(4)當
有意義;(4)當![]() __________時,
__________時,![]() 有意義.
有意義.
查看答案和解析>>
科目:初中數學 來源: 題型:
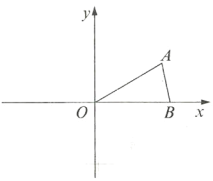
【題目】在平面直角坐標系中,A點坐標為(3,4),將線段OA繞原點O逆時針旋轉90°得到線段OA′,則點A′的坐標是( )
A. (﹣4,3) B. (﹣3,4)
C. (3,﹣4) D. (4,﹣3)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知等腰![]() 在平面直角坐標系中的位置如圖,點
在平面直角坐標系中的位置如圖,點![]() 坐標為
坐標為![]() ,點
,點![]() 坐標為
坐標為![]() .
.
(1)若將![]() 沿
沿![]() 軸向左平移
軸向左平移![]() 個單位,此時點
個單位,此時點![]() 恰好落在反比例函數
恰好落在反比例函數![]() 的圖像上,求
的圖像上,求![]() 的值;
的值;
(2)若將![]() 繞點
繞點![]() 順時針旋轉
順時針旋轉![]() ,點
,點![]() 恰好落在反比例函數
恰好落在反比例函數![]() 的圖像上,求
的圖像上,求![]() 的值;
的值;
(3)若將![]() 繞點
繞點![]() 順時針旋轉
順時針旋轉![]() 度
度![]() 到
到![]() 位置,當點
位置,當點![]() 、
、![]() 恰好同時落在(2)中所確定的反比例函數的圖像上時,請直接寫出經過點
恰好同時落在(2)中所確定的反比例函數的圖像上時,請直接寫出經過點![]() 、
、![]() 且以
且以![]() 軸為對稱的拋物線解析式.
軸為對稱的拋物線解析式.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系中,一次函數y=kx+b的圖象經過點A(﹣2,6),且與x軸相交于點B,與正比例函數y=3x的圖象相交于點C,點C的橫坐標為1.
(1)求k、b的值;
(2)若點D在y軸負半軸上,且滿足S△COD=![]() S△BOC,求點D的坐標.
S△BOC,求點D的坐標.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某專賣店有A、B兩種商品,已知在打折前,買60件A商品和30件B商品共用了1080元,買50件A商品和10件B商品共用了840元,A、B兩種商品打相同折以后,某人買500件A商品和450件B商品一共花了7840元,請你計算A、B商品打了多少折?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】有兩個可以自由轉動的均勻轉盤![]() ,都被分成了3等份,并在每份內均標有數字,如圖所示.規則如下:
,都被分成了3等份,并在每份內均標有數字,如圖所示.規則如下:
①分別轉動轉盤![]() ;
;
②兩個轉盤停止后,將兩個指針所指份內的數字相乘(若指針停止在等份線上,那么重轉一次,直到指針指向某一份為止).

【1】用列表法或樹狀圖分別求出數字之積為3的倍數和數字之積為5的倍數的概率;
【2】小明和小亮想用這兩個轉盤做游戲,他們規定:數字之積為3的倍數時,小明得2分;數字之積為5的倍數時,小亮得3分.這個游戲對雙方公平嗎?請說明理由;認為不公平的,試修改得分規定,使游戲對雙方公平.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】一項工程,甲,乙兩公司合做,12天可以完成,共需付施工費102000元;如果甲,乙兩公司單獨完成此項工程,乙公司所用時間是甲公司的1.5倍,乙公司每天的施工費比甲公司每天的施工費少1500元.
(1)甲,乙兩公司單獨完成此項工程,各需多少天?
(2)若讓一個公司單獨完成這項工程,哪個公司的施工費較少?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com