
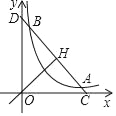
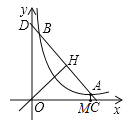
【題目】如圖,已知直線y=﹣x+b(b>0)與其垂線y=x交于H,與雙曲線c:y=![]() (k>0)在第一象限交于A,B,與兩坐標軸交于C,D.
(k>0)在第一象限交于A,B,與兩坐標軸交于C,D.
(1)當A的坐標為(2,1)時,求k的值和OH的長;
(2)若CH2﹣HA2=4,求雙曲線c的方程.
【答案】(1)OH=![]() ;(2)設雙曲線c的方程為y=
;(2)設雙曲線c的方程為y=![]() .
.
【解析】分析:(1)將A(2,1)代入y=![]() ,可得k=2,過A作AM⊥x軸于M,則AM=MC=1,OM=2,可得OC=OM+MC=3,依據∠HOC=45°,即可得到OH=
,可得k=2,過A作AM⊥x軸于M,則AM=MC=1,OM=2,可得OC=OM+MC=3,依據∠HOC=45°,即可得到OH=![]() OC=
OC=![]() ;
;
(2)設點A的坐標為(x,y)且x>y,則OC=OM+MC=x+y,OH=HC=![]() OC=
OC=![]() (x+y),進而得出HA=HC﹣AC=
(x+y),進而得出HA=HC﹣AC=![]() (x﹣y),根據CH2﹣HA2=[
(x﹣y),根據CH2﹣HA2=[![]() (x+y)]2﹣[
(x+y)]2﹣[![]() (x﹣y)]2=2xy=2k=4,即可得到k的值.
(x﹣y)]2=2xy=2k=4,即可得到k的值.
詳解:(1)將A(2,1)代入y=![]() ,可得:k=2×1=2,
,可得:k=2×1=2,
過A作AM⊥x軸于M,則AM=MC=1,OM=2,∴OC=OM+MC=3.
∵∠HOC=45°,∴OH=![]() OC=
OC=![]() ;
;
(2)設點A的坐標為(x,y)且x>y,則OC=OM+MC=x+y,OH=HC=![]() OC=
OC=![]() (x+y).
(x+y).
又∵AC=![]() AM=
AM=![]() y,∴HA=HC﹣AC=
y,∴HA=HC﹣AC=![]() (x﹣y).
(x﹣y).
∵CH2﹣HA2=[![]() (x+y)]2﹣[
(x+y)]2﹣[![]() (x﹣y)]2=2xy=2k=4,∴k=2,
(x﹣y)]2=2xy=2k=4,∴k=2,
∴雙曲線c的方程為y=![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:初中數學 來源: 題型:
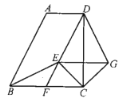
【題目】如圖所示,![]() ,
,![]() ,過點D作
,過點D作![]() ,交
,交![]() 的平分線于點E,連接BE,延長DE交BC于F,
的平分線于點E,連接BE,延長DE交BC于F,![]() .
.
(1)求證:![]() .
.
(2)將![]() 繞點C順時針旋轉
繞點C順時針旋轉![]() 得到
得到![]() ,連接EG.求證:CD垂直平分EG.
,連接EG.求證:CD垂直平分EG.
(3)延長BE交CD于點P,求證:P是CD的中點
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】網店店主小李進了一批某種商品,每件進價10元.預售一段時間后發現:每天銷售量![]() (件)與售價
(件)與售價![]() (元/件)之間成一次函數關系:
(元/件)之間成一次函數關系:![]() .
.
(1)小李想每天賺取利潤150元,又要使所進的貨盡快脫手,則售價定為多少合適?
(2)小李想每天賺取利潤300元,這個想法能實現嗎?為什么?
查看答案和解析>>
科目:初中數學 來源: 題型:
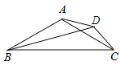
【題目】如圖:等腰△ABC中,AB=AC,點D在AC右側,∠BAC=∠BDC=120°
(1)猜想DA,DC,DB的數量關系并證明
(2)點D 在AB邊左側時三條線段關系是否發生變化?請畫出圖形。若變化,直接寫出結論.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知正方形ABCD,對角線的交點M(2,2).規定“把正方形ABCD先沿x軸翻折,再向左平移1個單位”為一次變換.如此這樣,連續經過2014次變換后,正方形ABCD的對角線交點M的坐標變為( )
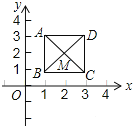
A. (﹣2012,2)B. (﹣2012,﹣2)C. (﹣2013,﹣2)D. (﹣2013,2)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】2019年4月23日,是第23個世界讀書日.為了推進中華傳統文化教育,營造濃厚的讀書氛圍,我市某學校舉辦了“讓讀書成為習慣,讓書香溢病校園”主題活動.為了解學生每周閱讀時間,該校隨機抽取了部分學生進行調查,根據調查結果,將閱詼時間![]() (單位:小時)分成了
(單位:小時)分成了![]() 組,
組, ![]()
![]()
![]() ,下圖是根據這組數據繪制的兩幅不完整的統計圖.請你結合圖中所給信息解答下列問題:
,下圖是根據這組數據繪制的兩幅不完整的統計圖.請你結合圖中所給信息解答下列問題:
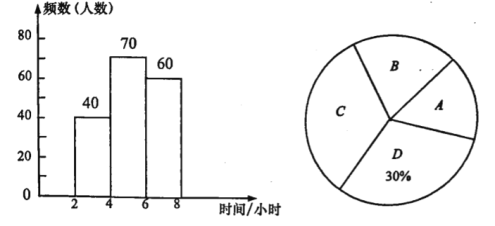
(1)這次隨機抽取了 名學生進行調查;
(2)補全頻數分布直方圖;
(3)計算扇形統計圖中扇形![]() 的圓心角的度數;
的圓心角的度數;
(4)若該校共有![]() 名學生,請你估計每周閱讀時間不足
名學生,請你估計每周閱讀時間不足![]() 小時的學生共有多少名?
小時的學生共有多少名?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,要得到DG∥BC,則需要條件( )
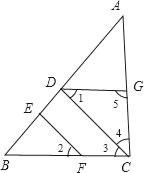
A. CD⊥AB,EF⊥AB B. ∠1=∠2
C. ∠1=∠2,∠4+∠5=180° D. CD⊥AB,EF⊥AB,∠1=∠2
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知拋物線![]()
![]() 與
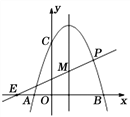
與![]() 軸交于A(-1,0),B(3,0)兩點,與
軸交于A(-1,0),B(3,0)兩點,與![]() 軸交于點C(0,3),動點P在拋物線上,直線PE與拋物線的對稱軸交于點M,點E的坐標為(-2,0).
軸交于點C(0,3),動點P在拋物線上,直線PE與拋物線的對稱軸交于點M,點E的坐標為(-2,0).
(1)求拋物線的函數表達式;
(2)若P與C關于拋物線的對稱軸對稱,求直線PE的函數表達式;
(3)若PM=![]() EM,求點P的坐標.
EM,求點P的坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:
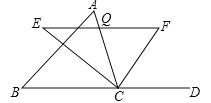
【題目】如圖,在△ABC中,點O是邊AC上一個動點,過點O作直線EF∥BC分別交∠ACB、外角∠ACD的平分線于點E、F.
(1)若CE=8,CF=6,求OC的長;
(2)連接AE、AF.問:當點O在邊AC上運動到什么位置時,四邊形AECF是矩形?并說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com