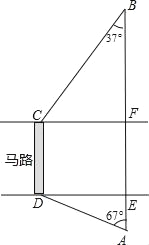
【題目】如圖，馬路的兩邊CF、DE互相平行，線段CD為人行橫道，馬路兩側的A、B兩點分別表示車站和超市，CD與AB所在直線互相平行，且都與馬路的兩邊垂直．馬路寬20米，A，B相距62米，∠A=67°，∠B=37°．求CD與AB之間的距離．（參考數據：sin67°≈
，cos67°≈
，tan67°≈
，sn37°≈
，cos37°≈
，tan37°≈
）
閱讀快車系列答案科目：初中數學 來源： 題型：
【題目】如圖，在
中，
，
，
于點D，點E是直線AC上一動點，連接DE，過點D作
，交直線BC于點F．
探究發現：
如圖1，若
，點E在線段AC上，則
______；
數學思考：
如圖2，若點E在線段AC上，則______
用含m，n的代數式表示
；
當點E在直線AC上運動時，中的結論是否任然成立？請僅就圖3的情形給出證明；
拓展應用：若
，
，
，請直接寫出CE的長．
查看答案和解析>>
科目：初中數學 來源： 題型：
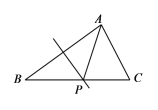
【題目】如圖，在
中，
.
⑴已知線段AB的垂直平分線與BC邊交于點P，連結AP，求證：
；
⑵以點B為圓心，線段AB的長為半徑畫弧，與BC邊交于點Q，連結AQ，若
，求
的度數.
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖1，OA=2，OB=4，以A點為頂點，AB為腰在第三象限作等腰直角△ABC.
（1）求C點的坐標.
（2）如圖2，OA=2,P為y軸負半軸上的一個動點，若以P為直角頂點，PA為腰作等腰直角△APD，過D作DE⊥x軸于E點，求OP－DE的值.
（3）如圖3，點F坐標為（－4，－4），點G（0，m）在y軸負半軸，點H（n，0）在x軸的正半軸，且FH⊥FG，求m+n的值.
查看答案和解析>>
科目：初中數學 來源： 題型：
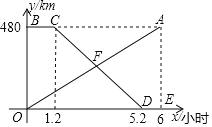
【題目】甲、乙兩地相距480km，一輛貨車從甲地勻速駛往乙地，貨車出發一段時間后，一輛汽車從乙地勻速駛往甲地，設貨車行駛的時間為
線段OA表示貨車離甲地的距離
與xh的函數圖象；折線BCDE表示汽車距離甲地的距離
與
的函數圖象．
求線段OA與線段CD所表示的函數表達式；
若OA與CD相交于點F，求點F的坐標，并解釋點F的實際意義；
當x為何值時，兩車相距100千米？
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，在等邊三角形ABC中，AB=AC=BC=10cm，DC=4cm。如果點M、N都以3cm/s的速度運動，點M在線段CB上由點C向點B運動，點N在線段BA上由點B向點A運動。它們同時出發，當兩點運動時間為t秒時，△BMN是一個直角三角形，則t的值為（ ）
A.
B.
C.
D.
查看答案和解析>>
科目：初中數學 來源： 題型：
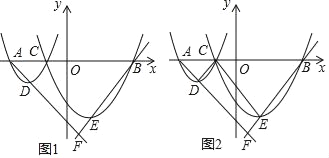
【題目】如圖1，在平面直角坐標系xOy中，已知A、B兩點的坐標分別為（﹣4，0）、（4，0），C（m，0）是線段AB上一動點（與A、B兩點不重合），拋物線l1：y=ax2+b1x+c1（a＞0）經過點A、C，頂點為D，拋物線l2：y=ax2+b2x+c2（a＞0）經過點C、B，頂點為E，直線AD、BE相交于F．
（1）若a=
，m=﹣1，求拋物線l1、l2的解析式；
（2）若a=1，∠AFB=90°，求m的值；
（3）如圖2，連接DC、EC，記△DAC的面積為S1，△ECB的面積為S2，△FAB的面積為S，問是否存在點C使得2S1S2=aS，若存在，請求出C的坐標；若不存在，請說明理由．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖①，在
中，
，
，
是過點
的一條直線，且點
在線段上時，
于點，
于點
.易證：
.
（1）如圖②，點在線段的延長線時，其余條件不變，問
與
，
的關系如何？請證明；
（2）如圖③，點在線段
的延長線時，其余條件不變，問與
的關系如何？請直接寫出結果，不需證明.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
