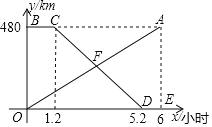
【題目】甲、乙兩地相距480km，一輛貨車從甲地勻速駛往乙地，貨車出發一段時間后，一輛汽車從乙地勻速駛往甲地，設貨車行駛的時間為
線段OA表示貨車離甲地的距離
與xh的函數圖象；折線BCDE表示汽車距離甲地的距離
與
的函數圖象．
求線段OA與線段CD所表示的函數表達式；
若OA與CD相交于點F，求點F的坐標，并解釋點F的實際意義；
當x為何值時，兩車相距100千米？
【答案】
線段OA對應的函數關系式為
，線段CD對應的函數關系式為
；
點F的坐標為
，點F的實際意義是：在貨車出發
小時時，距離甲地
千米，此時與汽車相遇；
x為
或
時，兩車相距100千米．
【解析】
根據函數圖象中的數據可以求得相應的函數解析式；
根據中的函數解析式可以求得點F的坐標，并寫出點F表示的實際意義；
根據題意可以得到相應的方程，從而可以解答本題．
設線段OA對應的函數關系式為
，
，得
，
即線段OA對應的函數關系式為，
設線段CD對應的函數關系式為
，
，得
，
即線段CD對應的函數關系式為；
，
解得，
，
點F的坐標為，點F的實際意義是：在貨車出發小時時，距離甲地千米，此時與汽車相遇；
由題意可得，
，
解得，
，
，
答：x為或時，兩車相距100千．
愉快的寒假南京出版社系列答案科目：初中數學 來源： 題型：
【題目】如圖1在△ABC中，∠ACB=90°，AC=BC，直線MN經過點C，且AD⊥MN于點D，BE⊥MN于點E．
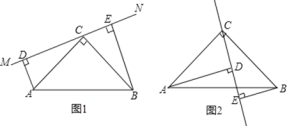
（1）求證：①△ADC≌△CEB；②DE=AD+BE．
（2）當直線MN繞點C旋轉到圖2的位置時，DE、AD、BE又怎樣的關系？并加以證明．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖,在等腰直角三角形ABC中,∠ABC=90°，D為AC邊中點，過D點作DE⊥DF，交AB于E，交BC于F.（1）求證：DE=DF.（2）若AE=8，FC=6，求EF長.
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，AB是⊙O的直徑，點F，C是⊙O上兩點，且F，C，B三等分半圓，連接AC，AF，過點C作CD⊥AF交AF延長線于點D，垂足為D．
（1）求證：CD是⊙O的切線；
（2）若CD=2
，求⊙O的半徑．
查看答案和解析>>
科目：初中數學 來源： 題型：
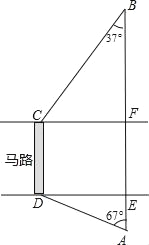
【題目】如圖，馬路的兩邊CF、DE互相平行，線段CD為人行橫道，馬路兩側的A、B兩點分別表示車站和超市，CD與AB所在直線互相平行，且都與馬路的兩邊垂直．馬路寬20米，A，B相距62米，∠A=67°，∠B=37°．求CD與AB之間的距離．（參考數據：sin67°≈
，cos67°≈
，tan67°≈
，sn37°≈
，cos37°≈
，tan37°≈
）
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，在ABCD中，
，
，
，點E為CD上一動點，經過A、C、E三點的
交BC于點F．
（操作與發現）
當E運動到
處，利用直尺與規作出點E與點F；
保留作圖痕跡
在的條件下，證明：
．
（探索與證明）
點E運動到任何一個位置時，求證：；
（延伸與應用）
點E在運動的過程中求EF的最小值．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】“低碳生活，綠色出行”,2017年1月,某公司向深圳市場新投放共享單車640輛.
(1)若1月份到4月份新投放單車數量的月平均增長率相同，3月份新投放共享單車1000輛.請問該公司4月份在深圳市新投放共享單車多少輛？
(2)考慮到自行車市場需求不斷增加,某商城準備用不超過70000元的資金再購進A，B兩種規格的自行車100輛，已知A型的進價為500元/輛，售價為700元/輛，B型車進價為1000元/輛，售價為1300元/輛。假設所進車輛全部售完，為了使利潤最大，該商城應如何進貨？
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，正方形網格中小方格邊長為1，請你根據所學的知識解決下面問題．
（1）求網格圖中△ABC的面積．
（2）判斷△ABC是什么形狀？并所明理由．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，等邊△ABD與等邊△ACE，連接BE、CD，BE的延長線與CD交于點F，下列結論：（1）BE=CD ；（2）AF平分∠EAC ； （3）∠BFD=60°；（4）AF+FD=BF 其中正確的有（ ）
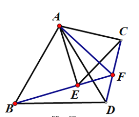
A.1個B.2個C.3個D.4個
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com