
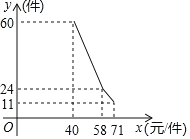
【題目】某店因為經營不善欠下38000元的無息貸款的債務,想轉行經營服裝專賣店又缺少資金.“中國夢想秀”欄目組決定借給該店30000元資金,并約定利用經營的利潤償還債務(所有債務均不計利息)已知該店代理的某品牌服裝的進價為每件40元,該品牌服裝日的售量y(件)與銷售價x(元/件)之間的關系可用圖中的一條折線(實線)來表示.
(1)求日銷售量y(件)與銷售價x(元/件)之間的函數關系式;
(2)當銷售價為多少元時,該店的日銷售利潤最大;
(3)該店每天支付工資和其它費用共250元,該店能否在一年內還清所有債務.
【答案】(1)![]() ;(2)當銷售價為55元時,該店的日銷售利潤最大,最大利潤為450元;(3)該店能在一年內還清所有債務.
;(2)當銷售價為55元時,該店的日銷售利潤最大,最大利潤為450元;(3)該店能在一年內還清所有債務.
【解析】
(1)利用待定系數法,即可求得日銷售量y(件)與銷售價x(元/件)之間的函數關系式
(2)根據銷售利潤=銷售量×(售價﹣進價),列出每天的銷售利潤w(元)與銷售價x(元/件)之間的函數關系式,再依據函數的增減性求得最大利潤.
(3)根據(2)中的最大利潤,可求得除去其他支出的利潤,即可判斷能否在一年內還清所有債務
(1)由圖象可得:
當40≤x<58時,設y=k1x+b1,把(40,60),(58,24)代入得
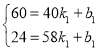 ,解得:
,解得: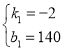 ,
,
∴y=﹣2x+140(40≤x<58)
當58≤x≤71時,設y=k2x+b2,把(58,24),(71,11)代入得
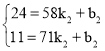 ,解得:
,解得: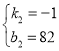 ,
,
∴y=﹣x+82(58≤x≤71)
故日銷售量y(件)與銷售價x(元/件)之間的函數關系為:![]() ;
;
(2)由(1)得
利潤w=![]()
整理得w=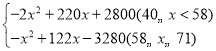
故當40≤x<58時,w=﹣2(x﹣55)2+450
∵﹣2<0,
∴當x=55時,有最大值450元
當58≤x≤71時,w=﹣(x﹣61)2+441
∵﹣1<0,
∴當x=61時,有最大值441元
綜上可得當銷售價為55元時,該店的日銷售利潤最大,最大利潤為450元
(3)由(2)可知每天的最大利潤為450元,
則有450﹣250=200元
一年的利潤為:200×365=73000元
所有債務為:30000+38000=68000元
∵73000>68000,
∴該店能在一年內還清所有債務.


科目:初中數學 來源: 題型:
【題目】如圖,![]() 是
是![]() 的直徑,四邊形
的直徑,四邊形![]() 是矩形,
是矩形,![]() 是
是![]() 上的點,
上的點,![]() ,與
,與![]() 交于點
交于點![]() ,己知
,己知![]() ,
,![]() 的半徑為30.
的半徑為30.
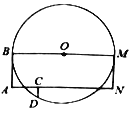
(1)求![]() 的長.
的長.
(2)連接![]() ,若將扇形
,若將扇形![]() 卷成一個圓錐,求這個圓錐底面半徑的長.
卷成一個圓錐,求這個圓錐底面半徑的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,拋物線![]() 交
交![]() 軸于
軸于![]() 兩點,交
兩點,交![]() 軸于點
軸于點![]() .直線
.直線![]() 經過點
經過點![]() .
.
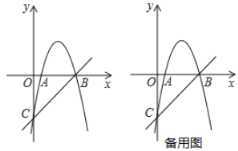
(1)求拋物線的解析式;
(2)若點![]() 為拋物線上動點,當
為拋物線上動點,當![]() 時,求點
時,求點![]() 的坐標,
的坐標,
(3)過點![]() 的直線交直線
的直線交直線![]() 于點
于點![]() 當
當![]() 時,過拋物線上一動點
時,過拋物線上一動點![]() (不與點
(不與點![]() 重合),作直線
重合),作直線![]() 的平行線交直線
的平行線交直線![]() 于點
于點![]() 若以點
若以點![]() 為頂點的四邊形是平行四邊形,求點
為頂點的四邊形是平行四邊形,求點![]() 的橫坐標.
的橫坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在平面直角坐標系xOy中,已知P(x1,y1)Q(x2,y2),定義P、Q兩點的橫坐標之差的絕對值與縱坐標之差的絕對值的和為P、Q兩點的直角距離,記作d(P,Q).即d(P,Q)=|x2﹣x1|+|y2﹣y1|
如圖1,在平面直角坐標系xOy中,A(1,4),B(5,2),則d(A,B)=|5﹣1|+|2﹣4|=6.
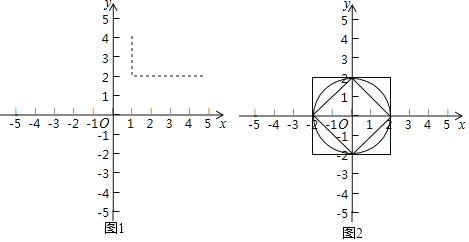
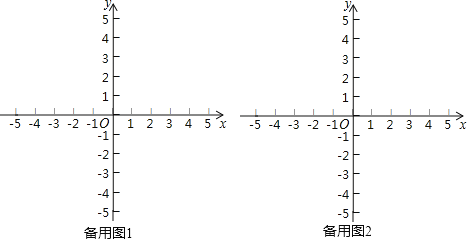
(1)如圖2,已知以下三個圖形:
①以原點為圓心,2為半徑的圓;
②以原點為中心,4為邊長,且各邊分別與坐標軸垂直的正方形;
③以原點為中心,對角線分別在兩條坐標軸上,對角線長為4的正方形.
點P是上面某個圖形上的一個動點,且滿足d(O,P)=2總成立.寫出符合題意的圖形對應的序號 .
(2)若直線y=k(x+3)上存在點P使得d(O,P)=2,求k的取值范圍.
(3)在平面直角坐標系xOy中,P為動點,且d(O,P)=3,⊙M圓心為M(t,0),半徑為1.若⊙M上存在點N使得PN=1,求t的取值范圍.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某校舉行“漢字聽寫”比賽,每位學生聽寫漢字40個,比賽結束后隨機抽查部分學生聽寫“正確的字數”,以下是根據抽查結果繪制的統計圖表.
頻數分布表
組別 | 正確的字數 | 人數 |
| 0.5~8.5 | 10 |
| 8.5~16.5 | 15 |
| 16.5~24.5 | 25 |
| 24.5~32.5 |
|
| 32.5~40.5 |
|
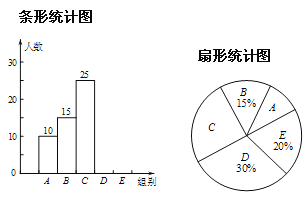
根據以上信息解決下列問題:
(1)補全條形統計圖;
(2)扇形統計圖中“![]() 組”所對應的圓心角的度數是_________;
組”所對應的圓心角的度數是_________;
(3)若該校共有1210名學生,如果聽寫正確的字數少于25,則定為不合格;請你估計這所學校本次比賽聽寫不合格的學生人數.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,△ABC中,∠C=90°,∠A=30°.

(1)用尺規作圖作AB邊上的中垂線DE,交AC于點D,交AB于點E.(保留作圖痕跡,不要求寫作法和證明);
(2)連接BD,求證:BD平分∠CBA.
查看答案和解析>>
科目:初中數學 來源: 題型:
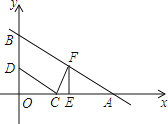
【題目】如圖,在平面直角坐標系中,一次函數圖象與x軸,y軸分別交于點A(8,0),B(0,4),點C的坐標為(3,0),動點D是射線BO上一個動點,連結CD,過點C作CD⊥FC,交一次函數圖象于點F.
(1)求這個一次函數的解析式;
(2)過點F作FE⊥x軸,垂足為點E,當△OCD與△EFC全等時,求出滿足條件的點F的坐標;
(3)點D在運動過程中,是否存在使△ACF是等腰三角形?若存在請求出點F的坐標;不存在,請說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com