
【題目】如圖,BD為△ABC外接圓⊙O的直徑,且∠BAE=∠C.
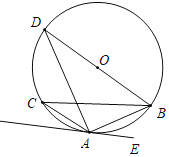
(1)求證:AE與⊙O相切于點A;
(2)若AE∥BC,BC=8,AB=2![]() ,求⊙O的半徑.
,求⊙O的半徑.
【答案】(1)見解析;(2)5
【解析】
(1)連接OA,根據圓周角定理、等腰三角形的性質和已知,求出∠DAO=∠BAE,∠DAB=90°,求出OAE=90,根據切線的判定得出即可;
(2)根據垂徑定理求出BF,根據勾股定理求出AF,再根據勾股定理求出OB即可.
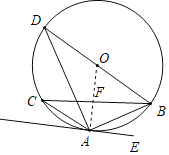
(1)連接OA交BC于點F,
∵OA=OD,
∴∠D=∠DAO,
∵由圓周角定理得:∠D=∠C,
∴∠C=∠DAO,
又∵∠C=∠BAE,
∴∠DAO=∠BAE,
∵BD為⊙O的直徑,
∴∠DAB=∠DAO+∠OAB=90°,
∴∠OAB+∠BAE=90°,即OA⊥AE,
∵OA是半徑,
∴AE與⊙O相切于點A;
(2)∵AE∥BC,AE⊥OA,
∴OA⊥BC,
∴FB=![]() BC=
BC=![]() ×8=4,
×8=4,
∴在Rt△ABF中,AF=![]() =
=![]() =2,
=2,
∵在Rt△OFB中,OB2=BF2+OF2,
∴OB2=42+(0B﹣2)2,
∴OB=5,
∴⊙O的半徑為5.


科目:初中數學 來源: 題型:
【題目】某農科所在相同條件下做某種作物種子發芽率的試驗,結果如表所示:
種子個數n | 1000 | 1500 | 2500 | 4000 | 8000 | 15000 | 20000 | 30000 |
發芽種子個數m | 899 | 1365 | 2245 | 3644 | 7272 | 13680 | 18160 | 27300 |
發芽種子頻率 | 0.899 | 0.910 | 0.898 | 0.911 | 0.909 | 0.912 | 0.908 | 0.910 |
則該作物種子發芽的概率約為_____________.(保留一位小數)
查看答案和解析>>
科目:初中數學 來源: 題型:
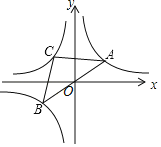
【題目】如圖,已知A,B為反比例函數y1=![]() 圖象上兩點,連接AB,線段AB經過點O,C是反比例函數y2=
圖象上兩點,連接AB,線段AB經過點O,C是反比例函數y2=![]() (k<0)在第二象限內的圖象上一點,當△CAB是以AB為底的等腰三角形,且
(k<0)在第二象限內的圖象上一點,當△CAB是以AB為底的等腰三角形,且![]() 時,k的值為( )
時,k的值為( )
A.﹣![]() B.﹣3C.﹣4D.﹣
B.﹣3C.﹣4D.﹣![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
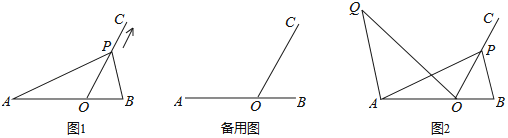
【題目】如圖1,點O在線段AB上,AO=4,OB=2,OC為射線,且∠BOC=60°,動點P以每秒2個單位長度的速度從點O出發,沿射線OC做運動,設運動時間為t秒.
(1)當t=1秒時,則OP= ,S△ABP= ;
(2)當△ABP是直角三角形時,求t的值;
(3)如圖2,當AP=AB時,過點A作AQ∥BP,并使得∠QOP=∠B,求AQBP的值.為了求AQBP的值,小華同學嘗試過O點作OE∥AP交BP于點E,試利用小華同學給我們的啟發補全圖形并求AQBP的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
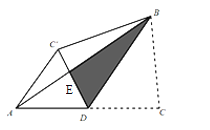
【題目】如圖,在△ABC中,D是AC邊上的中點,連結BD,把△BDC′沿BD翻折,得到△![]() ,DC與AB交于點E,連結
,DC與AB交于點E,連結![]() ,若AD=AC′=2,BD=3則點D到BC的距離為( )
,若AD=AC′=2,BD=3則點D到BC的距離為( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,矩形ABCD中,E是AD的中點,延長CE,BA交于點F,連接AC,DF.
(1)求證:四邊形ACDF是平行四邊形;
(2)當CF平分∠BCD時,寫出BC與CD的數量關系,并說明理由.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】若一個整數的個位數字截去,再從余下的數中,減去個位數的2倍,如果差是7的倍數,則原數能被7整除,如果差太大或心算不易看出是否7的倍數,就需要繼續上述[截尾、倍大、相減、驗差]的過程,直到能清楚判斷為止.
例如,判斷126是否7的倍數的過程如下:
12﹣6×2=0,0是7的倍數,所以126是7的倍數;
又例如判斷6789是否7的倍數的過程如下:
678﹣9×2=660,66﹣0×2=66,66不是7的倍數,所以6789不是7的倍數.
(1)請判斷2019和2555是否能被7整除,并說明理由;
(2)有一個千位數字是1的四位正整數,百位數字與十位數字的和是7,個位數字是十位數字的3倍,且這個四位正整數是7的倍數,求這個四位正整數.
查看答案和解析>>
科目:初中數學 來源: 題型:
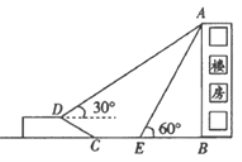
【題目】如圖,在一次綜合實踐活動中,小亮要測量一樓房的高度,先在坡面D處測得樓房頂部A的仰角為300 ,沿坡面向下走到坡腳C處,然后在地面上沿CB向樓房方向繼續行走10米到達E處,測得樓房頂部A的仰角為600 .已知坡面CD=10米,山坡的坡度![]() (坡度 是指坡面的鉛直高度與水平寬度的比),
(坡度 是指坡面的鉛直高度與水平寬度的比),
(1)求點D離地面高度(即點D到直線BC的距離);
(2)求樓房AB高度.(結果保留根式)
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com