
【題目】若一個整數的個位數字截去,再從余下的數中,減去個位數的2倍,如果差是7的倍數,則原數能被7整除,如果差太大或心算不易看出是否7的倍數,就需要繼續上述[截尾、倍大、相減、驗差]的過程,直到能清楚判斷為止.
例如,判斷126是否7的倍數的過程如下:
12﹣6×2=0,0是7的倍數,所以126是7的倍數;
又例如判斷6789是否7的倍數的過程如下:
678﹣9×2=660,66﹣0×2=66,66不是7的倍數,所以6789不是7的倍數.
(1)請判斷2019和2555是否能被7整除,并說明理由;
(2)有一個千位數字是1的四位正整數,百位數字與十位數字的和是7,個位數字是十位數字的3倍,且這個四位正整數是7的倍數,求這個四位正整數.
【答案】(1)2019不能被7整除,2555能被7整除,理由見解析;(2)這個四位正整數為1526.
【解析】
(1)根據題中方法及例題可知判斷2019是否能被7整除只需將201﹣9×2=183,18﹣3×2=12,看12能否被7整除即可,2555同理;
(2)設這個四位數的十位數字為x,由題意可得百位數字為7﹣x,個位數字為3x,由個十百位數字的范圍可求出0≤x≤3,又因為這四位正整數是7的倍數,這個四位數可以整除7,結果為整數,由此可求出x的值,即可知這四位數.
(1)2019不能被7整除,2555能被7整除,理由如下:
∵201﹣9×2=183,18﹣3×2=12,12不是7的倍數
∴2019不能被7整除
∵255﹣5×2=245,24﹣5×2=14,14是7的倍數
∴2555能被7整除
(2)設這個四位數的十位數字為x,則百位數字為7﹣x,個位數字為3x,則
0≤x≤9,0≤7﹣x≤9,0≤3x≤9
∴0≤x≤3
![]() =
=![]() =
=![]() =﹣12x+243﹣
=﹣12x+243﹣![]()
∵這個四位數能被7整除
∴![]() 為整數
為整數
∵0≤x≤3
∴x=2,7﹣x=5,3x=6
∴這個四位正整數為1526.


科目:初中數學 來源: 題型:
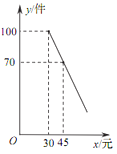
【題目】某商店購進一批成本為每件 30 元的商品,經調查發現,該商品每天的銷售量 y(件)與銷售單價 x(元)之間滿足一次函數關系,其圖象如圖所示.
(1)求該商品每天的銷售量 y 與銷售單價 x 之間的函數關系式;
(2)若商店按單價不低于成本價,且不高于 50 元銷售,則銷售單價定為多少,才能使銷售該商品每天獲得的利潤 w(元)最大?最大利潤是多少?
(3)若商店要使銷售該商品每天獲得的利潤不低于 800 元,則每天的銷售量最少應為多少件?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,BD為△ABC外接圓⊙O的直徑,且∠BAE=∠C.
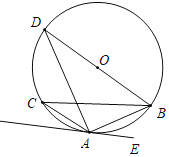
(1)求證:AE與⊙O相切于點A;
(2)若AE∥BC,BC=8,AB=2![]() ,求⊙O的半徑.
,求⊙O的半徑.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】從﹣3,﹣2,﹣1,0,1,2,3這七個數中,隨機抽取一個數記為m,若數m使關于x的分式方程![]() ﹣1=
﹣1=![]() 的解是非負數,且使得二次函數y=(m﹣2)x2+2x+1的圖象與x軸有交點,那么滿足條件所有m之和是( )
的解是非負數,且使得二次函數y=(m﹣2)x2+2x+1的圖象與x軸有交點,那么滿足條件所有m之和是( )
A.4B.3C.2D.1
查看答案和解析>>
科目:初中數學 來源: 題型:
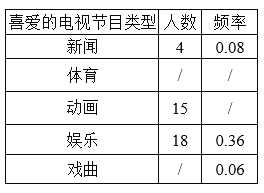
【題目】某校為了解學生對新聞、體育、動畫、娛樂、戲曲五類電視節目的喜愛情況,隨機選取該校部分學生進行調查,要求每名學生從中只選一類最喜愛的電視節目,以下是根據調查結果繪制的不完整統計表,根據表中信息,回答下列問題:
(1)本次共調查了______名學生;
(2)若將各類電視節目喜愛的人數所占比例繪制成扇形統計圖,則“喜愛體育”對應扇形的圓心角度數是_________度;
(3)該校共有1500名學生,根據調查結果估計該校“喜愛體育”節目的學生人數.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某校為了解全校![]() 名學生到校上學的方式,在全校隨機抽取了若干名學生進行問卷調查,問卷給出了五種上學方式供學生選擇,每人必選一項,且只能選一項.請根據下面兩個不完整的統計圖回答以下問題:
名學生到校上學的方式,在全校隨機抽取了若干名學生進行問卷調查,問卷給出了五種上學方式供學生選擇,每人必選一項,且只能選一項.請根據下面兩個不完整的統計圖回答以下問題:

(1)在這次調查中,共抽取了多少名學生;
(2)補全兩個統計圖;
(3)估計全校所有學生中有多少人乘坐公交車上學.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,拋物線y=ax2+bx+c經過點A(0,﹣3)、B(﹣1,0)、C(2,﹣3),拋物線與x軸的另一交點為點E,點P為拋物線上一動點,設點P的橫坐標為t.
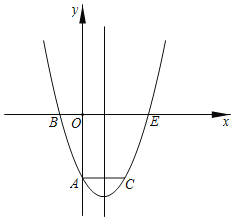
(1)求拋物線的解析式;
(2)若點P在第一象限,點M為拋物線對稱軸上一點,當四邊形MBEP恰好是平行四邊形時,求點P的坐標;
(3)若點P在第四象限,連結PA、PE及AE,當t為何值時,△PAE的面積最大?最大面積是多少?
(4)是否存在點P,使△PAE為以AE為直角邊的直角三角形,若存在,直接寫出點P的坐標;若不存在,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】反比例函數![]() 在第一象限的圖象如圖所示,過點A(1,0)作x軸的垂線,交反比例函數
在第一象限的圖象如圖所示,過點A(1,0)作x軸的垂線,交反比例函數![]() 的圖象于點M,△AOM的面積為3.
的圖象于點M,△AOM的面積為3.

(1)求反比例函數的解析式;
(2)設點B的坐標為(t,0),其中t>1.若以AB為一邊的正方形有一個頂點在反比例函數![]() 的圖象上,求t的值.
的圖象上,求t的值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com