
【題目】某單位需購買甲、乙兩種消毒劑.經了解,這兩種消毒劑的價格都有零售價和批發價(若按批發價,則每種消毒劑購買的數量不少于50桶),零售時甲種消毒劑每桶比乙種消毒劑多8元,已知購買兩種消毒劑各![]() (
(![]() )桶,所需費用分別是960元、720元.
)桶,所需費用分別是960元、720元.
(1)求甲、乙兩種消毒劑的零售價;
(2)該單位預計批發這兩種消毒劑500桶,且甲種消毒劑的數量不少于乙種消毒劑數量的![]() ,甲、乙兩種消毒劑的批發價分別為20元/桶、16元/桶.設甲種消毒劑批發數量為
,甲、乙兩種消毒劑的批發價分別為20元/桶、16元/桶.設甲種消毒劑批發數量為![]() 桶,購買資金總額為
桶,購買資金總額為![]() (元),請寫出
(元),請寫出![]() 與
與![]() 的函數關系式,并求出
的函數關系式,并求出![]() 的最小值和此時的購買方案.
的最小值和此時的購買方案.
【答案】(1)甲種消毒劑零售價為32元/桶,則乙種消毒劑零售價為24元/桶;(2)![]() (
(![]() ),當
),當![]() 時,
時,![]() 元,此時批發甲種消毒劑125桶,乙種消毒劑375桶.
元,此時批發甲種消毒劑125桶,乙種消毒劑375桶.
【解析】
(1)設甲種消毒劑零售價為![]() 元/桶,則乙種消毒劑零售價為
元/桶,則乙種消毒劑零售價為![]() 元/桶.根據題意列出分式方程,解方程,驗根,得到答案;
元/桶.根據題意列出分式方程,解方程,驗根,得到答案;
(2)根據![]() ,得到x≥125,根據題意列出y關于x的一次函數,判斷函數增減性,根據x取值范圍得到y的最小值,確定方案即可.
,得到x≥125,根據題意列出y關于x的一次函數,判斷函數增減性,根據x取值范圍得到y的最小值,確定方案即可.
(1)設甲種消毒劑零售價為![]() 元/桶,則乙種消毒劑零售價為
元/桶,則乙種消毒劑零售價為![]() 元/桶.
元/桶.
依題意:![]()
解得:![]() ,
,
經檢驗,![]() 是原方程的解,
是原方程的解,
∴![]() ,
,
即甲種消毒劑零售價為32元/桶,則乙種消毒劑零售價為24元/桶.
故答案為:甲種消毒劑零售價為32元/桶,則乙種消毒劑零售價為24元/桶
(2)依題意:![]() ,
,
解得:x≥125
又![]() ,
,
∵![]() ,
,
∴![]() 是增函數,y隨x的增大而增大
是增函數,y隨x的增大而增大
∵![]() ,
,
∴當![]() 時,
時,![]() (元)
(元)
此時批發甲種消毒劑125桶,乙種消毒劑375桶
故答案為:![]() (
(![]() ),當
),當![]() 時,
時,![]() 元,此時批發甲種消毒劑125桶,乙種消毒劑375桶.
元,此時批發甲種消毒劑125桶,乙種消毒劑375桶.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:初中數學 來源: 題型:
【題目】如圖,某旅游景區為方便游客,修建了一條東西走向的棧道AB,棧道AB與景區道路CD平行.在C處測得棧道一端A位于北偏西45°方向,在D處測得棧道另一端B位于北偏東32°方向.已知AC=60 m ,CD=46 m,求棧道AB的長(結果保留整數).參考數據:sin32° ≈ 0.53,cos32° ≈ 0.85,tan32° ≈ 0.62,![]() ≈ 1.414.
≈ 1.414.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】疫情期間部分學生選擇在家用電視觀看網絡課程,為了保護眼睛,電視機的安裝高度有一定的要求.如圖所示,小嘉家的壁掛電視機的安裝高度![]() 為1米,電視的中心位置
為1米,電視的中心位置![]() (
(![]() 的中點)比平視視線
的中點)比平視視線![]() 低
低![]() (這樣觀看眼睛最不容易疲勞),電視機寬度
(這樣觀看眼睛最不容易疲勞),電視機寬度![]() 為
為![]() ,眼到凳子平面的高度
,眼到凳子平面的高度![]() 為
為![]() .
.
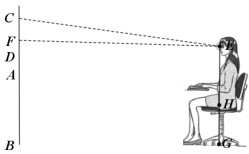
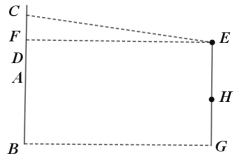
(1)求小嘉應選用凳子的高度;
(2)若看電視的視角![]() 為
為![]() 時,觀看感最好,求此時凳子中心
時,觀看感最好,求此時凳子中心![]() 到墻
到墻![]() 的距離(電視機的厚度忽略不計).(參考數據:
的距離(電視機的厚度忽略不計).(參考數據:![]() ,
,![]() ,
,![]() )
)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,點E是ABCD的邊CD的中點,連結AE并延長,交BC的延長線于點F.
(1)若AD的長為2.求CF的長.
(2)若∠BAF=90°,試添加一個條件,并寫出∠F的度數.
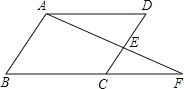
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖l,在![]() 中,
中,![]() ,
,![]() ,
,![]() 分別是邊
分別是邊![]() ,
,![]() 上的動點,且
上的動點,且![]() ,
,![]() 是
是![]() 的中點,連接
的中點,連接![]() ,
,![]() ,
,![]() ,設
,設![]() ,
,![]() 的面積為
的面積為![]() ,圖2是
,圖2是![]() 關于
關于![]() 的函數圖象,則下列說法不正確的是( )
的函數圖象,則下列說法不正確的是( )
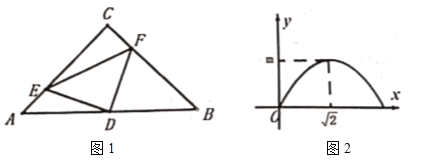
A.![]() 是等腰直角三角形B.
是等腰直角三角形B.![]()
C.![]() 的周長可以等于6D.四邊形
的周長可以等于6D.四邊形![]() 的面積為2
的面積為2
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】列方程或方程組解應用題:
北京市實施交通管理新措施以來,全市公共交通客運量顯著增加.據統計,2008年10月11日到2009年2月28日期間,地面公交日均客運量與軌道交通日均客運量總和為1696萬人次,地面公交日均客運量比軌道交通日均客運量的4倍少69萬人次.在此期間,地面公交和軌道交通日均客運量各為多少萬人次?
查看答案和解析>>
科目:初中數學 來源: 題型:
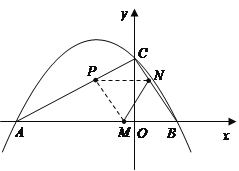
【題目】如圖,二次函數![]() (
(![]() )的圖象與
)的圖象與![]() 軸交于
軸交于![]() 兩點,與
兩點,與![]() 軸相交于點
軸相交于點![]() .連結
.連結![]() 兩點的坐標分別為
兩點的坐標分別為![]() 、
、![]() ,且當
,且當![]() 和
和![]() 時二次函數的函數值
時二次函數的函數值![]() 相等.
相等.
(1)求實數![]() 的值;
的值;
(2)若點![]() 同時從
同時從![]() 點出發,均以每秒1個單位長度的速度分別沿
點出發,均以每秒1個單位長度的速度分別沿![]() 邊運動,其中一個點到達終點時,另一點也隨之停止運動.當運動時間為
邊運動,其中一個點到達終點時,另一點也隨之停止運動.當運動時間為![]() 秒時,連結
秒時,連結![]() ,將
,將![]() 沿
沿![]() 翻折,
翻折,![]() 點恰好落在
點恰好落在![]() 邊上的
邊上的![]() 處,求
處,求![]() 的值及點
的值及點![]() 的坐標;
的坐標;
(3)在(2)的條件下,二次函數圖象的對稱軸上是否存在點![]() ,使得以
,使得以![]() 為項點的三角形與
為項點的三角形與![]() 相似?如果存在,請求出點
相似?如果存在,請求出點![]() 的坐標;如果不存在,請說明理由.
的坐標;如果不存在,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
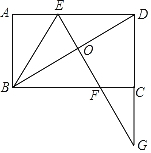
【題目】如圖,已知矩形ABCD,對角線BD的垂直平分線分別交AD,BC和BD于點E,F,O.EF,DC的延長線交于點G,且OD=CG,連接BE.
(1)求證:△DOE≌△GCF;
(2)求證:BE平分∠ABD.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com