
【題目】在△ABC中,∠A=90°,AB=4,AC=3,M是AB上的動點(不與A,B重合),過M點作MN∥BC交AC于點N.以MN為直徑作⊙O,并在⊙O內作內接矩形AMPN.令AM=x.
(1)用含x的代數式表示△MNP的面積S;
(2)當x為何值時,⊙O與直線BC相切;
(3)在動點M的運動過程中,記△MNP與梯形BCNM重合的面積為y,試求y關于x的函數表達式,并求x為何值時,y的值最大,最大值是多少?
【答案】
(1)
解:∵MN∥BC,
∴∠AMN=∠B,∠ANM=∠C.
∴△AMN∽△ABC.
∴ ![]() ,即
,即 ![]() ;
;
∴AN= ![]() x;
x;
∴S=S△MNP=S△AMN= ![]()
![]() xx=
xx= ![]() x2.(0<x<4)
x2.(0<x<4)
(2)
解:如圖2,設直線BC與⊙O相切于點D,連接AO,OD,則AO=OD= ![]() MN.
MN.
在Rt△ABC中,BC= ![]() =5;
=5;
由(1)知△AMN∽△ABC,
∴ ![]() ,即
,即 ![]() ,
,
∴MN= ![]() x
x
∴OD= ![]() x,
x,
過M點作MQ⊥BC于Q,則MQ=OD= ![]() x,
x,
在Rt△BMQ與Rt△BCA中,∠B是公共角,
∴△BMQ∽△BCA,
∴ ![]() ,
,
∴BM= ![]() x,AB=BM+MA=
x,AB=BM+MA= ![]() x+x=4
x+x=4
∴x= ![]() ,
,
∴當x= ![]() 時,⊙O與直線BC相切
時,⊙O與直線BC相切
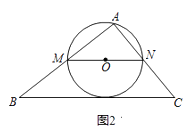
(3)
解:隨點M的運動,當P點落在直線BC上時,連接AP,則O點為AP的中點.
∵MN∥BC,
∴∠AMN=∠B,∠AOM=∠APB,
∴△AMO∽△ABP,
∴ ![]() ,
,
∵AM=MB=2,
故以下分兩種情況討論:
①當0<x≤2時,y=S△PMN= ![]() x2,
x2,
∴當x=2時,y最大= ![]() ×4=
×4= ![]() ,
,
②當2<x<4時,設PM,PN分別交BC于E,F,
∵四邊形AMPN是矩形,
∴PN∥AM,PN=M=x,
又∵MN∥BC,
∴四邊形MBFN是平行四邊形;
∴FN=BM=4﹣x,
∴PF=x﹣(4﹣x)=2x﹣4,
又∵△PEF∽△ACB,
∴ ![]() ,
,
∴S△PEF= ![]() (x﹣2)2;
(x﹣2)2;
y=S△MNP﹣S△PEF= ![]() x2﹣
x2﹣ ![]() (x﹣2)2=﹣
(x﹣2)2=﹣ ![]() x2+6x﹣6,
x2+6x﹣6,
當2<x<4時,y=﹣ ![]() x2+6x﹣6=﹣
x2+6x﹣6=﹣ ![]() (x﹣
(x﹣ ![]() )2+2,
)2+2,
∴當x= ![]() 時,滿足2<x<4,y最大=2.
時,滿足2<x<4,y最大=2.
綜上所述,當x= ![]() 時,y值最大,最大值是2
時,y值最大,最大值是2
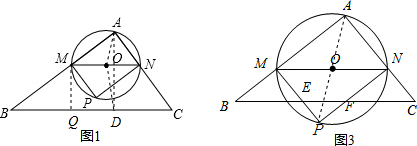
【解析】(1)由于三角形PMN和AMN的面積相當,那么可通過求三角形AMN的面積來得出三角形PMN的面積,求三角形AMN的面積可根據三角形AMN和ABC相似,根據相似比的平方等于面積比來得出三角形AMN的面積;(2)當圓O與BC相切時,O到BC的距離就是MN的一半,那么關鍵是求出MN的表達式,可根據三角形AMN和三角形ABC相似,得出MN的表達式,也就求出了O到BC的距離的表達式,如果過M作MQ⊥BC于Q,那么MQ就是O到BC的距離,然后在直角三角形BMQ中,用∠B的正弦函數以及BM的表達式表示出MQ,然后讓這兩表示MQ的含x的表達式相等,即可求出x的值;(3)要求重合部分的面積首先看P點在三角形ABC內部還是外面,因此可先得出這兩種情況的分界線即當P落到BC上時,x的取值,那么P落點BC上時,MN就是三角形ABC的中位線,此時AM=2,因此可分兩種情況進行討論:
①當0<x≤2時,此時重合部分的面積就是三角形PMN的面積,三角形PMN的面積(1)中已經求出,即可的x,y的函數關系式.②當2<x<4時,如果設PM,PN交BC于E,F,那么重合部分就是四邊形MEFN,可通過三角形PMN的面積﹣三角形PEF的面積來求重合部分的面積.不難得出PN=AM=x,而四邊形BMNF又是個平行四邊形,可得出FN=BM,也就有了FN的表達式,就可以求出PF的表達式,然后參照(1)的方法可求出三角形PEF的面積,即可求出四邊形MEFN的面積,也就得出了y,x的函數關系式.然后根據兩種情況得出的函數的性質,以及對應的自變量的取值范圍求出y的最大值即可.


科目:初中數學 來源: 題型:
【題目】如圖,M是△ABC的邊BC的中點,AN平分∠BAC,BN⊥AN于點N,延長BN交AC于點D,已知AB=10,BC=15,MN=3
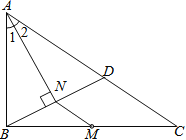
(1)求證:BN=DN;
(2)求△ABC的周長
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,AB為⊙O直徑,BC為⊙O切線,連接A、C兩點,交⊙O于點D,BE=CE,連接DE,OE. 
(1)判斷DE與⊙O的位置關系,并說明理由;
(2)求證:BC2=CD2OE;
(3)若cos∠BAD= ![]() ,BE=6,求OE的長.
,BE=6,求OE的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,把矩形紙片ABCD沿EF折疊,使點B落在邊AD上的點B′處,點A落在點A′處,已知AD=10,CD=4,B′D=2.
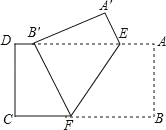
(1)求證:B′E=BF;
(2)求AE的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
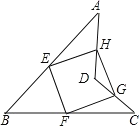
【題目】如圖,E. F. G、H分別是邊AB、BC、CD、DA的中點.
(1)判斷四邊形EFGH的形狀,并說明你的理由;
(2)連接BD和AC,當BD、AC滿足何條件時,四邊形EFGH是正方形?證明你的理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】解決問題:
一輛貨車從超市出發,向東走了3千米到達小彬家,繼續走2.5千米到達小穎家,然后向西走了10千米到達小明家,最后回到超市.
(1)以超市為原點,以向東的方向為正方向,用1個單位長度表示1千米,在數軸上表示出小明家,小彬家,小穎家的位置.
(2)小明家距小彬家多遠?
(3)貨車一共行駛了多少千米?
(4)貨車每千米耗油0.2升,這次共耗油多少升?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】小米是一個愛動腦筋的孩子,他用如下方法作∠AOB的角平分線: 作法:如圖,
⑴在射線OA上任取一點C,過點C作CD∥OB;
⑵以點C為圓心,CO的長為半徑作弧,交CD于點E;
⑶作射線OE.
所以射線OE就是∠AOB的角平分線.請回答:小米的作圖依據是 .
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】為了響應市委和市政府“綠色環保,節能減排”的號召,幸福商場用3300元購進甲、乙兩種節能燈共計100只,很快售完.這兩種節能燈的進價、售價如下表:
進價(元/只) | 售價(元/只) | |
甲種節能燈 | 30 | 40 |
甲種節能燈 | 35 | 50 |
(1)求幸福商場甲、乙兩種節能燈各購進了多少只?
(2)全部售完100只節能燈后,商場共計獲利多少元?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知拋物線y=ax2+bx+c的頂點為D(﹣1,2),其部分圖象如圖所示,給出下列四個結論: ①a<0; ②b2﹣4ac>0;③2a﹣b=0;④若點P(x0 , y0)在拋物線上,則ax02+bx0+c≤a﹣b+c.其中結論正確的是( )
A.1個
B.2個
C.3個
D.4個
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com