
【題目】我們知道平行四邊形那有很多性質,現在如果我們把平行四邊形沿著它的一條對角線翻折,會發現這其中還有更多的結論
(1)【發現與證明】
在ABCD中,AB≠BC,將△ABC沿AC翻折至△AB′C,連接B′D.
結論1:B′D∥AC;
結論2:△AB′C與ABCD重疊部分的圖形是等腰三角形.
…
請利用圖1證明結論1或結論2.
(2)【應用與探究】
在ABCD中,∠B=30°,將△ABC沿AC翻折至△AB′C,連接B′D.
如圖1,若AB= ![]() ,∠AB′D=75°,則∠ACB= , BC=;
,∠AB′D=75°,則∠ACB= , BC=;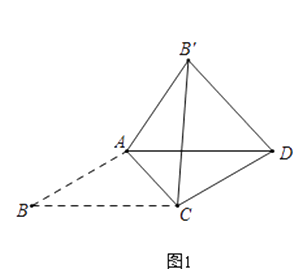
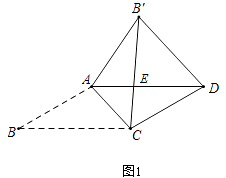
(3)如圖2,AB=2 ![]() ,BC=1,AB′與CD相交于點E,求△AEC的面積;
,BC=1,AB′與CD相交于點E,求△AEC的面積;
(4)已知AB=2 ![]() ,當BC的長為多少時,△AB′D是直角三角形?
,當BC的長為多少時,△AB′D是直角三角形?
【答案】
(1)
在ABCD中,AB≠BC,將△ABC沿AC翻折至△AB′C,連接B′D.
如圖1,∵四邊形ABCD是平行四邊形,
∴AB=CD,BC=AD,∠B=∠ADC,
∵將△ABC沿AC翻折至△AB′C,
∴AB′=AB,B′C=BC,∠AB′C=∠B,
∴AB′=CD,B′C=AD,∠AB′C=∠ADC,
在△AB′C和△CAD中,
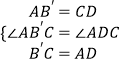 ,
,
∴△AB′C≌△CAD(SAS),
∴∠ACB′=∠CAD,
設AD、B′C相交于E,
∴AE=CE,
∴△ACE是等腰三角形,
即△AB′C與ABCD重疊部分的圖形是等腰三角形;
∵B′C=AD,AE=CE,
∴B′E=DE,
∴∠CB′D=∠ADB′,
∵∠AEC=∠B′ED,∠ACB′=∠CAD,
∴∠ADB′=∠DAC,
∴B′D∥AC;
(2)45°;![]()
(3)
解:如圖2,

作CG⊥AB′于G,
∵∠B=30°,
∴∠AB′C=30°,
∴CG= ![]() B′C=
B′C= ![]() BC=
BC= ![]() ,B′G=
,B′G= ![]() B′C=
B′C= ![]() BC=
BC= ![]() ,
,
∵AB′=AB=2 ![]() ,
,
∴AG=2 ![]() ﹣
﹣ ![]() =
= ![]() ,
,
設AE=CE=x,則EG= ![]() ﹣x,
﹣x,
∵CG2+EG2=CE2,
∴( ![]() )2+(
)2+( ![]() ﹣x)2=x2,解得x=
﹣x)2=x2,解得x= ![]() ,
,
∴AE= ![]() ,
,
∴△AEC的面積= ![]() AECG=
AECG= ![]() ×
× ![]() ×
× ![]() =
= ![]() ;
;
(4)
解:如圖2,∵AD=BC,BC=B′C,
∴AD=B′C,
∵AC∥B′D,
∴四邊形ACB′D是等腰梯形,
∵∠B=30°,
∴∠AB′C=∠CDA=30°,
∵△AB′D是直角三角形,
當∠B′AD=90°,AB>BC時,
設∠ADB′=∠CB′D=y,
∴∠AB′D=y﹣30°,
∵∠AB′D+∠ADB′=90°,
∴y﹣30°+y=90°,解得y=60°,
∴∠AB′D=y﹣30°=30°,
∵AB′=AB=2 ![]() ,
,
∴AD= ![]() ×2
×2 ![]() =2,
=2,
∴BC=2,
當∠ADB′=90°,AB>BC時,如圖3,

∵AD=BC,BC=B′C,
∴AD=B′C,
∵AC∥B′D,
∴四邊形ACB′D是等腰梯形,
∵∠ADB′=90°,
∴四邊形ACB′D是矩形,
∴∠ACB′=90°,
∴∠ACB=90°,
∵∠B=30°,AB=2 ![]() ,
,
∴BC= ![]() AB=
AB= ![]() ×2
×2 ![]() =3;
=3;
當∠B′AD=90°AB<BC時,如圖4,

∵AD=BC,BC=B′C,
∴AD=B′C,
∵AC∥B′D,∠B′AD=90°,
∴∠B′GC=90°,
∵∠B=30°,AB=2 ![]() ,
,
∴∠AB′C=30°,
∴GC= ![]() B′C=
B′C= ![]() BC,
BC,
∴G是BC的中點,
在RT△ABG中,BG= ![]() AB=
AB= ![]() ×2
×2 ![]() =3,
=3,
∴BC=6;
當∠AB′D=90°時,如圖5,

∵AD=BC,BC=B′C,
∴AD=B′C,
∵AC∥B′D,
∴四邊形ACDB′是等腰梯形,
∵∠AB′D=90°,
∴四邊形ACDB′是矩形,
∴∠BAC=90°,
∵∠B=30°,AB=2 ![]() ,
,
∴BC=AB÷ ![]() =2
=2 ![]() ×
× ![]() =4;
=4;
∴已知當BC的長為2或3或4或6時,△AB′D是直角三角形.
【解析】【發現與證明】通過三角形全等即可求得∠ACB′=∠CAD,即可得到結論2;進而根據等腰三角形的性質證得∠ADB′=∠DAC,根據平行線的判定即可證得結論1;【應用與探究】(1)根據對折的性質求得∠AB′C=30°,從而求得∠CB′D=45°,由于B′D∥AC,得出∠ACB′=∠CB′D=45°,進而即可求得∠ACB=45°;作AG⊥BC于G,根據解直角三角形即可求得BC;(2)作CG⊥AB′于G,通過解直角三角形求得CG= ![]() ,B′G=
,B′G= ![]() ,進而求得AG=2
,進而求得AG=2 ![]() ﹣
﹣ ![]() =
= ![]() ,設AE=CE=x,則EG=
,設AE=CE=x,則EG= ![]() ﹣x,根據勾股定理即可求得x值,即AE的值,然后根據三角形的面積公式即可求得△AEC的面積;(3)先證得四邊形ACB′D是等腰梯形,根據等腰梯形的性質得出∠AB′C=∠CDA=30°,∠B′AD=∠DCB′=90°,設∠ADB′=∠CB′D=y,則∠AB′D=y﹣30°,根據∠AB′D+∠ADB′=90°,得出y﹣30°+y=90°,解得y=60°,進而求得∠AB′D=30°,通過解直角三角形即可求得BC.
﹣x,根據勾股定理即可求得x值,即AE的值,然后根據三角形的面積公式即可求得△AEC的面積;(3)先證得四邊形ACB′D是等腰梯形,根據等腰梯形的性質得出∠AB′C=∠CDA=30°,∠B′AD=∠DCB′=90°,設∠ADB′=∠CB′D=y,則∠AB′D=y﹣30°,根據∠AB′D+∠ADB′=90°,得出y﹣30°+y=90°,解得y=60°,進而求得∠AB′D=30°,通過解直角三角形即可求得BC.
【應用與探究】(1)如圖1,∵在ABCD中,∠B=30°,將△ABC沿AC翻折至△AB′C,
∴∠AB′C=30°,
∵∠AB′D=75°,
∴∠CB′D=45°,
∵B′D∥AC,
∴∠ACB′=∠CB′D=45°,
∵∠ACB=∠ACB′,
∴∠ACB=45°;
作AG⊥BC于G,
∴AG=CG,
∵∠B=30°,
∴AG= ![]() AB=
AB= ![]()
![]() =
= ![]() ,
,
∴CG= ![]() ,BG=
,BG= ![]() =
= ![]() ,
,
∴BC=BG+CG= ![]() ,
,
所以答案是:45°, ![]() ;
;
【考點精析】本題主要考查了平行四邊形的判定的相關知識點,需要掌握兩組對邊分別平行的四邊形是平行四邊形:兩組對邊分別相等的四邊形是平行四邊形;一組對邊平行且相等的四邊形是平行四邊形;兩組對角分別相等的四邊形是平行四邊形;對角線互相平分的四邊形是平行四邊形才能正確解答此題.


科目:初中數學 來源: 題型:
【題目】甲、乙兩位同學參加數學綜合素質測試,各項成績如下(單位:分)
數與代數 | 空間與圖形 | 統計與概率 | 綜合與實踐 | |
學生甲 | 90 | 93 | 89 | 90 |
學生乙 | 94 | 92 | 94 | 86 |
(1)分別計算甲、乙成績的中位數;
(2)如果數與代數、空間與圖形、統計與概率、綜合與實踐的成績按3:3:2:2計算,那么甲、乙的數學綜合素質成績分別為多少分?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,將ABCD的邊AB延長到點E,使BE=AB,連接DE,交邊BC于點F. 
(1)求證:△BEF≌△CDF;
(2)連接BD、CE,若∠BFD=2∠A,求證:四邊形BECD是矩形.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知過點(2,﹣3)的直線y=ax+b(a≠0)不經過第一象限,設s=a+2b,則s的取值范圍是( )
A.﹣5≤s≤﹣ ![]()
B.﹣6<s≤﹣ ![]()
C.﹣6≤s≤﹣ ![]()
D.﹣7<s≤﹣ ![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在平面直角坐標系xOy中,直線y=kx+4(k≠0)與y軸交于點A.
(1)如圖,直線y=﹣2x+1與直線y=kx+4(k≠0)交于點B,與y軸交于點C,點B的橫坐標為﹣1. ①求點B的坐標及k的值;
②直線y=﹣2x+1與直線y=kx+4與y軸所圍成的△ABC的面積等于;
(2)直線y=kx+4(k≠0)與x軸交于點E(x0 , 0),若﹣2<x0<﹣1,求k的取值范圍.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知矩形ABCD的一條邊AD=8,將矩形ABCD折疊,使得頂點B落在CD邊上的P點處.
(1)如圖1,已知折痕與邊BC交于點O,連結AP、OP、OA. ①求證:△OCP∽△PDA;
②若△OCP與△PDA的面積比為1:4,求邊AB的長;
(2)若圖1中的點P恰好是CD邊的中點,求∠OAB的度數;
(3)如圖2, ![]()
![]()
![]()
![]()
![]()
![]() ,擦去折痕AO、線段OP,連結BP.動點M在線段AP上(點M與點P、A不重合),動點N在線段AB的延長線上,且BN=PM,連結MN交PB于點F,作ME⊥BP于點E.試問當點M、N在移動過程中,線段EF的長度是否發生變化?若變化,說明理由;若不變,求出線段EF的長度.
,擦去折痕AO、線段OP,連結BP.動點M在線段AP上(點M與點P、A不重合),動點N在線段AB的延長線上,且BN=PM,連結MN交PB于點F,作ME⊥BP于點E.試問當點M、N在移動過程中,線段EF的長度是否發生變化?若變化,說明理由;若不變,求出線段EF的長度. 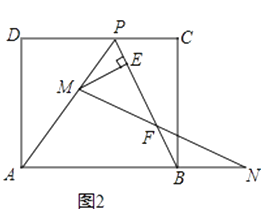
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,矩形ABCD的邊AB=3cm,AD=4cm,點E從點A出發,沿射線AD移動,以CE為直徑作圓O,點F為圓O與射線BD的公共點,連接EF、CF,過點E作EG⊥EF,EG與圓O相交于點G,連接CG. 
(1)試說明四邊形EFCG是矩形;
(2)當圓O與射線BD相切時,點E停止移動,在點E移動的過程中, ①矩形EFCG的面積是否存在最大值或最小值?若存在,求出這個最大值或最小值;若不存在,說明理由;
②求點G移動路線的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,港口A在觀測站O的正東方向,OA=4km,某船從港口A出發,沿北偏東15°方向航行一段距離后到達B處,此時從觀測站O處測得該船位于北偏東60°的方向,則該船航行的距離(即AB的長)為( )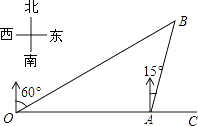
A.4km
B.2 ![]() km
km
C.2 ![]() km
km
D.( ![]() +1)km
+1)km
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com