
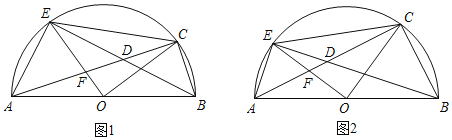
【題目】如圖,AB是半圓O的直徑,C為半圓弧上一點(diǎn),在AC上取一點(diǎn)D,使BC=CD,連結(jié)BD并延長交⊙O于E,連結(jié)AE,OE交AC于F.
(1)求證:△AED是等腰直角三角形;
(2)如圖1,已知⊙O的半徑為![]() .
.
①求![]() 的長;
的長;
②若D為EB中點(diǎn),求BC的長.
(3)如圖2,若AF:FD=7:3,且BC=4,求⊙O的半徑.
【答案】(1)見解析;(2)①![]() ;②
;②![]() ;(3)
;(3)![]()
【解析】
(1)由已知可得△BCD是等腰直角三角形,所以∠CBD=∠EAD=45°,因為∠AEB=90°可證△AED是等腰直角三角形;
(2)①已知可得∠EAD=45°,∠EOC=90°,則△EOC是等腰直角三角形,所以CE的弧長=![]() ×2×π×
×2×π×![]() =
=![]() ;
;
②由已知可得ED=BD,在Rt△ABE中,(2![]() )2=AE2+(2AE)2,所以AE=2,AD=2
)2=AE2+(2AE)2,所以AE=2,AD=2![]() ,易證△AED∽△BCD,所以BC=
,易證△AED∽△BCD,所以BC=![]() ;
;
(3)由已知可得AF=![]() AD,過點(diǎn)E作EG⊥AD于G,EG=
AD,過點(diǎn)E作EG⊥AD于G,EG=![]() AD,GF=
AD,GF=![]() AD,tan∠EFG=
AD,tan∠EFG=![]() ,得出FO=
,得出FO=![]() r,在Rt△COF中,FC=
r,在Rt△COF中,FC=![]() r,EF=
r,EF=![]() r,在Rr△EFG中,由勾股定理,求出AD=
r,在Rr△EFG中,由勾股定理,求出AD=![]() r,AF=
r,AF=![]() r,所以AC=AF+FC=
r,所以AC=AF+FC=![]() ,CD=BC=4,AC=4+AD,可得
,CD=BC=4,AC=4+AD,可得![]() r=4+
r=4+![]() r,解出r即可.
r,解出r即可.
解:(1)∵BC=CD,AB是直徑,
∴△BCD是等腰直角三角形,
∴∠CBD=45°,
∵∠CBD=∠EAD=45°,
∵∠AEB=90°,
∴△AED是等腰直角三角形;
(2)①∵∠EAD=45°,
∴∠EOC=90°,
∴△EOC是等腰直角三角形,
∵⊙O的半徑為![]() ,
,
∴CE的弧長=![]() ×2×π×
×2×π×![]() =
=![]() ,
,
故答案為:![]() ;
;
②∵D為EB中點(diǎn),
∴ED=BD,
∵AE=ED,
在Rt△ABE中,(2![]() )2=AE2+(2AE)2,
)2=AE2+(2AE)2,
∴AE=2,
∴AD=2![]() ,
,
∵ED=AE,CD=BC,∠AED=∠BCD=90°,
∴△AED∽△BCD,
∴BC=![]() ,
,
故答案為:![]() ;
;
(3)∵AF:FD=7:3,
∴AF=![]() AD,
AD,
過點(diǎn)E作EG⊥AD于G,
∴EG=![]() AD,
AD,
∴GF=![]() AD,
AD,
∴tan∠EFG=![]() ,
,
∴![]() =
=![]() =
=![]() ,
,
∴FO=![]() r,
r,
在Rt△COF中,FC=![]() r,
r,
∴EF=![]() r,
r,
在Rt△EFG中,(![]() r)2=(
r)2=(![]() AD)2+(
AD)2+(![]() AD)2,
AD)2,
∴AD=![]() r,
r,
∴AF=![]() r,
r,
∴AC=AF+FC=![]() r,
r,
∵CD=BC=4,
∴AC=4+AD=4+![]() r,
r,
∴![]() r=4+
r=4+![]() r,
r,
∴r=![]() ,
,
故答案為:![]() .
.


 導(dǎo)學(xué)全程練創(chuàng)優(yōu)訓(xùn)練系列答案
導(dǎo)學(xué)全程練創(chuàng)優(yōu)訓(xùn)練系列答案
| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來源: 題型:
【題目】已知:如圖,![]() 和
和![]() 均為等腰直角三角形,
均為等腰直角三角形,![]() ,連結(jié)
,連結(jié)![]() ,
,![]() ,且
,且![]() 、
、![]() 、
、![]() 三點(diǎn)在一直線上,
三點(diǎn)在一直線上,![]() ,
,![]() .
.
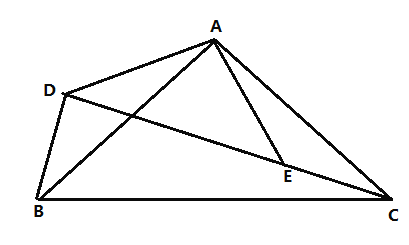
(1)求證:![]() ;
;
(2)求線段![]() 的長.
的長.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,在△ABC中,D是AB邊上任意一點(diǎn),E是BC邊中點(diǎn),過點(diǎn)C作AB的平行線,交DE的延長線于點(diǎn)F,連接BF,CD.
(1)求證:四邊形CDBF是平行四邊形;
(2)若∠FDB=30°,∠ABC=45°,BC=4![]() ,求DF的長.
,求DF的長.

查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】江蘇省第十九屆運(yùn)動會將于2018年9月在揚(yáng)州舉行開幕式,某校為了了解學(xué)生“最喜愛的省運(yùn)會項目”的情況,隨機(jī)抽取了部分學(xué)生進(jìn)行問卷調(diào)查,規(guī)定每人從“籃球”、“羽毛球”、“自行車”、“游泳”和“其他”五個選項中必須選擇且只能選擇一個,并將調(diào)查結(jié)果繪制成如下兩幅不完整的統(tǒng)計圖表.
最喜愛的省運(yùn)會項目的人數(shù)調(diào)查統(tǒng)計表


根據(jù)以上信息,請回答下列問題:
(1)這次調(diào)查的樣本容量是 ,![]() ;
;
(2)扇形統(tǒng)計圖中“自行車”對應(yīng)的扇形的圓心角為 度;
(3)若該校有1200名學(xué)生,估計該校最喜愛的省運(yùn)會項目是籃球的學(xué)生人數(shù).
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
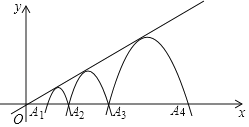
【題目】若二次函數(shù)的圖象與x軸的兩個交點(diǎn)和頂點(diǎn)構(gòu)成等邊三角形,則稱這樣的二次函數(shù)的圖象為標(biāo)準(zhǔn)拋物線.如圖,自左至右的一組二次函數(shù)的圖象T1,T2,T3……是標(biāo)準(zhǔn)拋物線,且頂點(diǎn)都在直線y=![]() x上,T1與x軸交于點(diǎn)A1(2,0),A2(A2在A1右側(cè)),T2與x軸交于點(diǎn)A2,A3,T3與x軸交于點(diǎn)A3,A4,……,則拋物線Tn的函數(shù)表達(dá)式為_____.
x上,T1與x軸交于點(diǎn)A1(2,0),A2(A2在A1右側(cè)),T2與x軸交于點(diǎn)A2,A3,T3與x軸交于點(diǎn)A3,A4,……,則拋物線Tn的函數(shù)表達(dá)式為_____.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
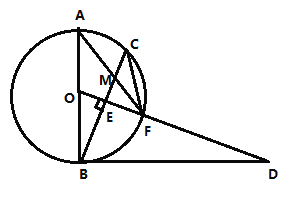
【題目】如圖,![]() 是
是![]() 的直徑,
的直徑,![]() 為
為![]() 上一點(diǎn),
上一點(diǎn),![]() 于點(diǎn)
于點(diǎn)![]() ,交
,交![]() 于點(diǎn)
于點(diǎn)![]() ,
,![]() 與
與![]() 交于點(diǎn)
交于點(diǎn)![]() 為
為![]() 延長線上一點(diǎn),且
延長線上一點(diǎn),且![]() .
.
(1)求證:![]() 是
是![]() 的切線;
的切線;
(2)求證:![]() ;
;
(3)若![]() ,求
,求![]() 的長.
的長.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,在△ABC 中,AB=AC,AE 是∠BAC 的平分線,∠ABC 的平分線 BM 交 AE 于點(diǎn) M,點(diǎn) O在 AB 上,以點(diǎn)O 為圓心,OB 的長為半徑的圓經(jīng)過點(diǎn) M,交 BC 于點(diǎn)G,交 AB 于點(diǎn) F.
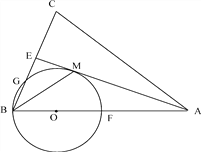
(1)求證:AE 為⊙O 的切線.
(2)當(dāng) BC=8,AC=12 時,求⊙O 的半徑.
(3)在(2)的條件下,求線段 BG 的長.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
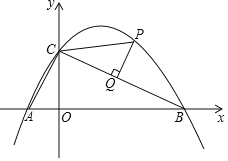
【題目】如圖,二次函數(shù)![]() 的圖像與
的圖像與![]() 軸相交于點(diǎn)A(-1,0),B(4,0),與
軸相交于點(diǎn)A(-1,0),B(4,0),與![]() 軸相交于點(diǎn)C.
軸相交于點(diǎn)C.
(1)求該函數(shù)的表達(dá)式;
(2)若點(diǎn)P(2,m)為該函數(shù)在第一象限內(nèi)的圖象上一點(diǎn),過點(diǎn)P作PQ⊥BC,垂足為點(diǎn)Q,連接PC,求線段PQ的長;
(3)在(2)的條件下,點(diǎn)M為該函數(shù)圖象上一點(diǎn),且∠MAP=45°,求點(diǎn)M的坐標(biāo).

查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】已知a、b、c為正數(shù),若關(guān)于x的一元二次方程ax2+bx+c=0有兩個實數(shù)根,則關(guān)于x的方程a2x2+b2x+c2=0解的情況為( )
A.有兩個不相等的正根B.有一個正根,一個負(fù)根
C.有兩個不相等的負(fù)根D.不一定有實數(shù)根
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com