
【題目】已知在![]() 中,∠C=90°,AC=8,BC=6,
中,∠C=90°,AC=8,BC=6,
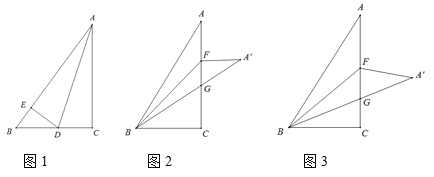
(1)若AD是∠BAC的角平分線,AD交BC邊于D,過點D作DE⊥AB與點E(如圖1),請求出BE的長及![]() 的值;
的值;
(2)點F是邊AC上的一點,連接BF,把![]() 沿著直線BF對折得到
沿著直線BF對折得到![]() ,
,![]() 與AC交于點G,若BC=CF,如圖2,請證明
與AC交于點G,若BC=CF,如圖2,請證明![]() ∽
∽![]() ;
;
(3)點F是邊AC上的一點,連接BF,把![]() 沿著直線BF對折得到
沿著直線BF對折得到![]() ,
,![]() 與AC交于點G,若
與AC交于點G,若![]() ,如圖3,請求出
,如圖3,請求出![]() 的值(可以直接利用第(1)題求出的結論)
的值(可以直接利用第(1)題求出的結論)
【答案】(1)![]() ;
; ![]() ;(2)見解析;(3)
;(2)見解析;(3)![]()
【解析】
(1)設CD=DE=x,則BD=6-x,通過![]() 是
是![]() 的角平分線,
的角平分線,![]() ,
,![]() ,證明△ADE≌△ADC(AAS),可得CD=DE,AE=AC=8,推出
,證明△ADE≌△ADC(AAS),可得CD=DE,AE=AC=8,推出![]() ,再根據勾股定理構建方程即可解決問題.
,再根據勾股定理構建方程即可解決問題.
(2)設![]() 的度數為
的度數為![]() ,由折疊可得
,由折疊可得![]() ,根據
,根據![]() ,
,![]() ,
,
可得![]() ,利用折疊和三角形的外角的性質,可得
,利用折疊和三角形的外角的性質,可得![]() ,則可證
,則可證![]() ∽
∽![]()
(3)作A′H⊥AC于H,設![]() 的長度為
的長度為![]() ,利用
,利用![]() ≌
≌![]() ,
,![]() ∥
∥![]() ,得到
,得到![]() ,由(1)得
,由(1)得![]() ,則
,則![]() ,解得
,解得![]() ,則有
,則有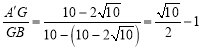 .
.
解:∵∠C=90°,AC=8,BC=6,
∴AB=10,
(1)設![]() 的長度為
的長度為![]() ,則
,則![]()
∵![]() 是
是![]() 的角平分線,
的角平分線,![]() ,
,![]()
∴![]() ,
,
又∵![]() ,
,![]() ,
,
∴![]() ≌
≌![]() (AAS)
(AAS)
∴![]()
∴![]()
在直角![]() 中,
中,![]()
∴![]()
解得![]()
∴![]()
綜上所述,![]() ,
,![]()
(2)設![]() 的度數為
的度數為![]() ,由折疊可得
,由折疊可得![]()
∵![]() ,
,![]()
∴![]()
∴![]()
∵![]()
∴![]()
∴![]()
∴![]()
又∵![]()
∴![]() ∽
∽![]()
(3)如圖,過點![]() 作
作![]() 交
交![]() 于
于![]() 點,
點,
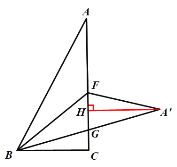
設![]() 的長度為
的長度為![]() ,由折疊可得
,由折疊可得![]() ≌
≌![]()
∴![]() ,
,![]() ,
,![]() ,
,
∵![]() ,
,![]()
∴![]()
∴![]()
∵![]()
∴![]() ∥
∥![]()
∴![]()
由(1)得![]()
∴![]()
∴![]()
解得![]()
∴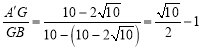


科目:初中數學 來源: 題型:
【題目】某企業安排65名工人生產甲、乙兩種產品,每人每天生產2件甲或1件乙,甲產品每件可獲利15元。根據市場需求,乙產品每天產量不少于5件,當每天生產5件時,每件可獲利120元,每增加1件,當天平均每件利潤減少2元,設每天安排![]() 人生產乙產品。
人生產乙產品。
(1)根據信息填表:
產品種類 | 每天工人數(人) | 每天產量(件) | 每件產品可獲利潤(元) |
甲 | — | — | 15 |
乙 |
|
| — |
(2)該企業在不增加工人的情況下,增加生產丙產品,要求每天甲、丙兩種產品的產量相等,已知每人每天可生產1件丙(每人每天只能生產一件產品),丙產品每件可獲利30元,求每天生產三種產品可獲得的總利潤![]() (元)的最大值及相應的
(元)的最大值及相應的![]() 值。
值。
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】4件同型號的產品中,有1件不合格品和3件合格品.
(1)從這4件產品中隨機抽取1件進行檢測,求抽到的是不合格品的概率;
(2)從這4件產品中隨機抽取2件進行檢測,求抽到的都是合格品的概率;
(3)在這4件產品中加入x件合格品后,進行如下試驗:隨機抽取1件進行檢測,然后放回,多次重復這個試驗,通過大量重復試驗后發現,抽到合格品的頻率穩定在0.95,則可以推算出x的值大約是多少?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系中,矩形OABC頂點A、C分別在x軸、y軸的正半軸上,頂點B在反比例函數y=![]() (x>0)的圖象上,點P是矩形OABC內的一點,連接PO、PA、PB、PC,若圖中陰影部分的面積10,則k為__.
(x>0)的圖象上,點P是矩形OABC內的一點,連接PO、PA、PB、PC,若圖中陰影部分的面積10,則k為__.
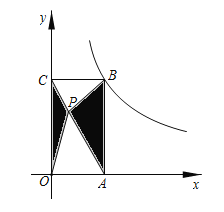
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知△ABC和△DCE是等邊三角形,連接BE,連接DA并延長交CE于點F,交BE于點G,CD=6,EF=2,那么EG的長為__________.
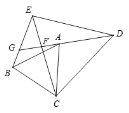
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知拋物線y=ax2+bx+c經過A(-1,0)、B(3,0)、C(0,3)三點,直線l是拋物線的對稱軸.
(1)求拋物線的函數關系式;
(2)設點P是直線l上的一個動點,當△PAC的周長最小時,求點P的坐標;
(3)在直線l上是否存在點M,使△MAC為等腰三角形?若存在,直接寫出所有符合條件的點M的坐標;若不存在,請說明理由.
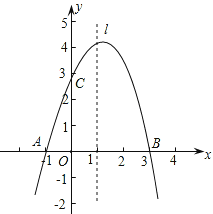
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在矩形ABCD中,AB=3,AD=8,O為AD中點,P是線段AO上一動點,以O為圓心,OP為半徑作⊙O分別交BO及BO延長線于點E,F,延長AE交BC于點H.
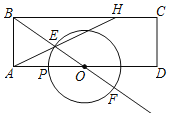
(1)當OP=2時,求BH的長.
(2)當AH交⊙O于另一點G時,連接FG,DF,作DM⊥BF于點M,求證:△EFG∽△FDM.
(3)連結HO,當△EHO是直角三角形時,求OP的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
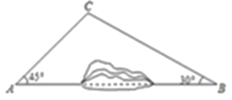
【題目】為加快城鄉對接,建設美麗鄉村,某地區對A、B兩地間的公路進行改建.如圖,A、B兩地之間有一座山.汽車原來從A地到B地需途徑C地沿折線ACB行駛,現開通隧道后,汽車可直接沿直線AB行駛.已知BC=100千米,∠A=45°,∠B=30°.
(1)開通隧道前,汽車從A地到B地要走多少千米?
(2)開通隧道后,汽車從A地到B地可以少走多少千米?(結果保留根號)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在△ABC中,∠C=90°,∠BAC的平分線交BC于點D,點O在AB上,以點O為圓心,OA為半徑的圓恰好經過點D,分別交AC,AB于點E,F.
(1)試判斷直線BC與⊙O的位置關系,并說明理由;
(2)若BD=2![]() ,BF=2,求陰影部分的面積(結果保留π).
,BF=2,求陰影部分的面積(結果保留π).

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com