
【題目】如圖所示,梯形![]() 的頂點
的頂點![]() 、
、![]() 在反比例函數
在反比例函數![]() 圖像上,
圖像上,![]() ,上底邊
,上底邊![]() 在直線
在直線![]() 上,下底邊
上,下底邊![]() 交
交![]() 軸于
軸于![]() ,點
,點![]() 的縱坐標是1.
的縱坐標是1.
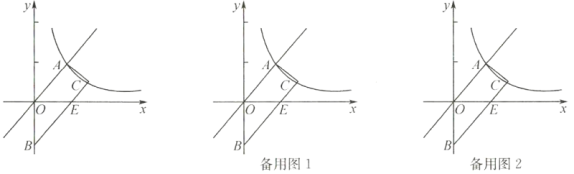
(1)求反比例函數的解析式;
(2)求四邊形![]() 的面積;
的面積;
(3)若將點![]() 的坐標改為
的坐標改為![]() ,且
,且![]() ,其他條件不變,探究四邊形
,其他條件不變,探究四邊形![]() 的面積;
的面積;
(4)若將點![]() 的坐標改為
的坐標改為![]() ,且
,且![]() ,點
,點![]() 的縱坐標改為
的縱坐標改為![]() ,且
,且![]() ,其他條件不變,直接寫出四邊形
,其他條件不變,直接寫出四邊形![]() 的面積.
的面積.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() ;(4)
;(4)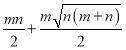
【解析】
(1)如圖所示,過點![]() ,
,![]() 分別作
分別作![]() 軸的垂線,垂足分別為
軸的垂線,垂足分別為![]() ,
,![]() ,由于上底邊在直線y=x上,故可得出
,由于上底邊在直線y=x上,故可得出![]() ,
,![]() ,然后結合題意可求得點C坐標,進而可得結果;
,然后結合題意可求得點C坐標,進而可得結果;
(2)先聯立![]() 與
與![]() 組成方程組,解方程組即得點A坐標,即為AM和OM的長,然后利用S四邊形AOEC=S△AOM+S梯形AMNC-S△CEN代入相關數據求解即可;
組成方程組,解方程組即得點A坐標,即為AM和OM的長,然后利用S四邊形AOEC=S△AOM+S梯形AMNC-S△CEN代入相關數據求解即可;
(3)根據題意可求得點C坐標,進而可得反比例函數關系式,然后仿(2)的思路求出點A坐標,再利用S四邊形AOEC=S△AOM+S梯形AMNC-S△CEN代入相關數據求解即可;
(4)根據題意可求得點C坐標,進而可得反比例函數關系式,然后仿(3)的思路求出點A坐標,再利用S四邊形AOEC=S△AOM+S梯形AMNC-S△CEN代入相關數據求解即可.
(1)如圖所示,過點![]() ,
,![]() 分別作
分別作![]() 軸的垂線,垂足分別為
軸的垂線,垂足分別為![]() ,
,![]() ,
,
∵OA在直線y=x上,∴![]() ,
,
∵![]() ,∴
,∴![]() ,
,
∵點![]() 的縱坐標為1,∴
的縱坐標為1,∴![]() ,
,
∵![]() ,∴
,∴![]() ,
,
∴點![]() 的坐標為
的坐標為![]() ,
,
∴![]() ,即
,即![]() ;
;
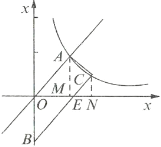
(2)將![]() 與
與![]() 組成方程組得
組成方程組得![]() ,解得
,解得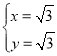 ,或
,或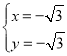 (舍去),
(舍去),
∴AM=OM=![]() ,將
,將![]() 代入
代入![]() 得:
得:![]() ,即
,即![]() 點的橫坐標為3,
點的橫坐標為3,
∴![]() ,
,
∴S四邊形AOEC=S△AOM+S梯形AMNC-S△CEN![]() .
.
(3)∵點![]() 的縱坐標為1,點
的縱坐標為1,點![]() ,∴點
,∴點![]() .
.
∵點![]() 在反比例函數的圖像上,∴
在反比例函數的圖像上,∴![]() ,
,
解方程組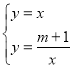 ,得
,得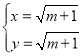 ,或
,或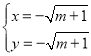 (舍去),
(舍去),
∴點![]() 的坐標為
的坐標為![]() .
.
∴S四邊形AOEC=S△AOM+S梯形AMNC-S△CEN ![]()
![]() ;
;

(4)∵點![]() 的縱坐標為n,點
的縱坐標為n,點![]() ,∴點
,∴點![]() .
.
∵點![]() 在反比例函數的圖像上,∴
在反比例函數的圖像上,∴![]() ,
,
解方程組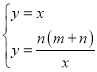 ,得
,得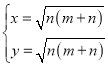 ,或
,或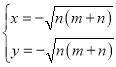 (舍去),
(舍去),
∴S四邊形AOEC=S△AOM+S梯形AMNC-S△CEN![]()
![]() .
.


 勵耘書業暑假銜接寧波出版社系列答案
勵耘書業暑假銜接寧波出版社系列答案科目:初中數學 來源: 題型:
【題目】如圖,在![]() 中,
中,![]() ,
,![]() 是
是![]() 的中點。在射線
的中點。在射線![]() 上任意取一點
上任意取一點![]() ,連接
,連接![]() ,將線段
,將線段![]() 繞點
繞點![]() 逆時針方向旋轉80°,點
逆時針方向旋轉80°,點![]() 的對應點是點
的對應點是點![]() ,連接
,連接![]() .
.
(1)如圖1,當點![]() 落在射線
落在射線![]() 上時,
上時,
①![]() _________________°;
_________________°;
②直線![]() 與直線
與直線![]() 的位置關系是______________________。
的位置關系是______________________。

(2)如圖2,當點![]() 落在射線
落在射線![]() 的左側時,試判斷直線
的左側時,試判斷直線![]() 與直線
與直線![]() 的位置關系,并證明你的結論。
的位置關系,并證明你的結論。

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】甲、乙兩人同時從A地前往相距5千米的B地,甲騎自行車,途中修車耽誤了20分鐘,甲行駛的路程s(千米)關于時間t(分鐘)的函數圖像如圖所示;乙慢跑所行的路程s(千米)關于時間t(分鐘)的函數解析式為![]()
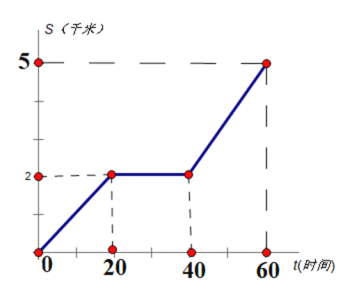
(1)在圖中畫出乙慢跑所行的路程關于時間的函數圖像:
(2)甲修車后行駛的速度是每分鐘_______米;
(3)甲、乙兩人在出發后,中途_________分鐘時相遇
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,Rt△ABO的頂點A是反比例函數y=![]() 與一次函數y=﹣x﹣(k+1)的圖象在第二象限的交點,AB⊥x軸于B,且S△ABO=
與一次函數y=﹣x﹣(k+1)的圖象在第二象限的交點,AB⊥x軸于B,且S△ABO=![]() .
.
(1)直接寫出這兩個函數的關系式;
(2)求△AOC的面積;
(3)根據圖象直接寫出:當x為何值時,反比例函數的值小于一次函數的值.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某彈簧掛上不超過20千克的物體后按一定規律伸長,測得一彈簧的長度![]() (厘米)與所掛的物體的質量
(厘米)與所掛的物體的質量![]() (千克)有下面的關系:
(千克)有下面的關系:
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 12 | 12.5 | 13 | 13.5 | 14 | 14.5 | 15 | 15.5 | 16 |
那么彈簧的總長![]() (厘米)與所掛的物體的質量
(厘米)與所掛的物體的質量![]() (千克)之間是否是函數關系?若是,請寫出函數關系式.
(千克)之間是否是函數關系?若是,請寫出函數關系式.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖Rt△ABC中∠ACB=90°,將其折疊使點A落在邊BC的點A′處,折痕為CD,若∠A′DB=20°,則∠B=( )
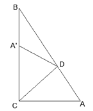
A.45°B.35°C.30°D.40°
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在△ABC中,AB=2AC, 點D在BC上,且∠CAD=∠B,點E是AB的中點,聯結CE與AD交于點G,點F在BC上,且∠CEF=∠BAC.
(1)若∠BAC=90°,如圖1,求證: EG+ EF=![]() AC;
AC;
(2)若∠BAC=120°,如圖2,請猜想線段EG,EF和AC之間的數量關系并證明.
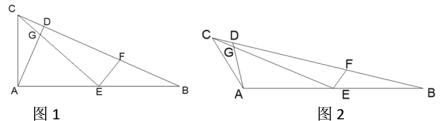
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com