
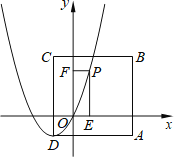
【題目】如圖,在正方形ABCD中,點(diǎn)A的坐標(biāo)為(![]() ,
,![]() ),點(diǎn)D的坐標(biāo)為(
),點(diǎn)D的坐標(biāo)為(![]() ,
,![]() ),且AB∥y軸,AD∥x軸. 點(diǎn)P是拋物線
),且AB∥y軸,AD∥x軸. 點(diǎn)P是拋物線![]() 上一點(diǎn),過點(diǎn)P作PE⊥x軸于點(diǎn)E,PF⊥y軸于點(diǎn) F.
上一點(diǎn),過點(diǎn)P作PE⊥x軸于點(diǎn)E,PF⊥y軸于點(diǎn) F.
(1)直接寫出點(diǎn)![]() 的坐標(biāo);
的坐標(biāo);
(2)若點(diǎn)P在第二象限,當(dāng)四邊形PEOF是正方形時(shí),求正方形PEOF的邊長;
(3)以點(diǎn)E為頂點(diǎn)的拋物線![]() 經(jīng)過點(diǎn)F,當(dāng)點(diǎn)P在正方形ABCD內(nèi)部(不包含邊)時(shí),求a的取值范圍.
經(jīng)過點(diǎn)F,當(dāng)點(diǎn)P在正方形ABCD內(nèi)部(不包含邊)時(shí),求a的取值范圍.
【答案】(1)B (3,3);(2)正方形![]() 的邊長為3;(3)
的邊長為3;(3)![]() >3或
>3或![]() <
<![]() .
.
【解析】
(1)先利用A點(diǎn)和D點(diǎn)坐標(biāo)得到正方形ABCD的邊長為4,然后寫出B點(diǎn)坐標(biāo);
(2)設(shè)點(diǎn)P(x,x2+2x),利用正方形的性質(zhì)得到PE=PF,即x2+2x=-x,然后解方程求出x即可得到正方形PEOF的邊長;
(3)設(shè)P(m,m2+2m)(m≠0),則E(m,0),F(0,m2+2m),利用頂點(diǎn)式表示以E為頂點(diǎn)的拋物線解析式為y=a(x-m)2,再把F(0,m2+2m)代入得m=![]() ,接著求出拋物線y=x2+2x與BC的交點(diǎn)坐標(biāo)為(1,3),則利用點(diǎn)P在正方形ABCD內(nèi)部(不包含邊)得到-1<m<1且m≠0,然后分別解-1<
,接著求出拋物線y=x2+2x與BC的交點(diǎn)坐標(biāo)為(1,3),則利用點(diǎn)P在正方形ABCD內(nèi)部(不包含邊)得到-1<m<1且m≠0,然后分別解-1<![]() <0和0<
<0和0<![]() <1即可.
<1即可.
(1)![]() (
(![]() ,
,![]() );(2)設(shè)點(diǎn)
);(2)設(shè)點(diǎn)![]() (
(![]() ,
,![]() ).
).
當(dāng)四邊形![]() 是正方形時(shí),
是正方形時(shí),![]() ,
,
當(dāng)點(diǎn)![]() 在第二象限時(shí),有
在第二象限時(shí),有![]() .
.
解得![]() ,
,![]() .
.
∵![]() ,
,
∴![]() .
.
∴正方形![]() 的邊長為
的邊長為![]() .
.
(3)設(shè)點(diǎn)![]() (
(![]() ,
,![]() ),則點(diǎn)E(
),則點(diǎn)E(![]() ,
,![]() ),則點(diǎn)F(
),則點(diǎn)F(![]() ,
,![]() ).
).
∵![]() 為拋物線頂點(diǎn),
為拋物線頂點(diǎn),
∴該拋物線解析式為![]() .
.
∵拋物線經(jīng)過點(diǎn)![]() ,
,
∴![]() ,化簡得
,化簡得![]() .
.
對于![]() ,令
,令![]() ,解得
,解得![]() ; 令
; 令![]() ,解得
,解得![]() .
.
∵點(diǎn)![]() 在正方形
在正方形![]() 內(nèi)部,
內(nèi)部,
∴![]() <
<![]() <
<![]() ,且
,且![]() .
.
①當(dāng)![]() <
<![]() <
<![]() 時(shí)
時(shí)
由反比例函數(shù)性質(zhì)知![]() ,∴
,∴![]() <
<![]() .
.
②當(dāng)![]() <
<![]() <
<![]() 時(shí)
時(shí)
由反比例函數(shù)性質(zhì)知![]() ,∴
,∴![]() >
>![]() .
.



| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來源: 題型:
【題目】為增強(qiáng)學(xué)生的身體素質(zhì),教育行政部門規(guī)定每位學(xué)生每天參加戶外活動(dòng)的平均時(shí)間不少于1小時(shí). 為了解學(xué)生參加戶外活動(dòng)的情況,對部分學(xué)生參加戶外活動(dòng)的時(shí)間進(jìn)行抽樣調(diào)查,并將調(diào)查結(jié)果繪制作成如下兩幅不完整的統(tǒng)計(jì)圖,
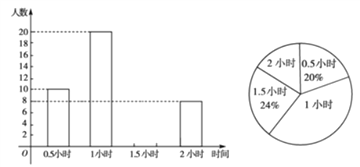
請你根據(jù)圖中提供的信息解答下列問題:
(1)在這次調(diào)查中共調(diào)查了多少名學(xué)生?
(2)求戶外活動(dòng)時(shí)間為1.5小時(shí)的人數(shù),并補(bǔ)充頻數(shù)分布直方圖;
(3)戶外活動(dòng)時(shí)間的眾數(shù)和中位數(shù)分別是多少?
(4)若該市共有20000名學(xué)生,大約有多少學(xué)生戶外活動(dòng)的平均時(shí)間符合要求?
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】問題發(fā)現(xiàn):
(![]() )如圖①,
)如圖①,![]() 中,
中,![]() ,
,![]() ,
,![]() ,點(diǎn)
,點(diǎn)![]() 是
是![]() 邊上任意一點(diǎn),則
邊上任意一點(diǎn),則![]() 的最小值為__________.
的最小值為__________.
(![]() )如圖②,矩形
)如圖②,矩形![]() 中,
中,![]() ,
,![]() ,點(diǎn)
,點(diǎn)![]() 、點(diǎn)
、點(diǎn)![]() 分別在
分別在![]() 、
、![]() 上,求
上,求![]() 的最小值.
的最小值.
(![]() )如圖③,矩形
)如圖③,矩形![]() 中,
中,![]() ,
,![]() ,點(diǎn)
,點(diǎn)![]() 是
是![]() 邊上一點(diǎn),且
邊上一點(diǎn),且![]() ,點(diǎn)
,點(diǎn)![]() 是
是![]() 邊上的任意一點(diǎn),把
邊上的任意一點(diǎn),把![]() 沿
沿![]() 翻折,點(diǎn)
翻折,點(diǎn)![]() 的對應(yīng)點(diǎn)為點(diǎn)
的對應(yīng)點(diǎn)為點(diǎn)![]() ,連接
,連接![]() 、
、![]() ,四邊形
,四邊形![]() 的面積是否存在最小值,若存在,求這個(gè)最小值及此時(shí)
的面積是否存在最小值,若存在,求這個(gè)最小值及此時(shí)![]() 的長度;若不存在,請說明理由.
的長度;若不存在,請說明理由.



查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】善于不斷改進(jìn)學(xué)習(xí)方法的小迪發(fā)現(xiàn),對解題進(jìn)行回顧反思,學(xué)習(xí)效果更好.某一天小迪有20分鐘時(shí)間可用于學(xué)習(xí).假設(shè)小迪用于解題的時(shí)間![]() (單位:分鐘)與學(xué)習(xí)收益量
(單位:分鐘)與學(xué)習(xí)收益量![]() 的關(guān)系如圖1所示,用于回顧反思的時(shí)間
的關(guān)系如圖1所示,用于回顧反思的時(shí)間![]() (單位:分鐘)與學(xué)習(xí)收益
(單位:分鐘)與學(xué)習(xí)收益![]() 的關(guān)系如圖2所示(其中
的關(guān)系如圖2所示(其中![]() 是拋物線的一部分,
是拋物線的一部分,![]() 為拋物線的頂點(diǎn)),且用于回顧反思的時(shí)間不超過用于解題的時(shí)間.
為拋物線的頂點(diǎn)),且用于回顧反思的時(shí)間不超過用于解題的時(shí)間.
(1)求小迪解題的學(xué)習(xí)收益量![]() 與用于解題的時(shí)間
與用于解題的時(shí)間![]() 之間的函數(shù)關(guān)系式;
之間的函數(shù)關(guān)系式;
(2)求小迪回顧反思的學(xué)習(xí)收益量![]() 與用于回顧反思的時(shí)間
與用于回顧反思的時(shí)間![]() 的函數(shù)關(guān)系式;
的函數(shù)關(guān)系式;
(3)問小迪如何分配解題和回顧反思的時(shí)間,才能使這20分鐘的學(xué)習(xí)收益總量最大?
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】現(xiàn)在,蘇寧商場進(jìn)行促銷活動(dòng),出售一種優(yōu)惠購物卡(注:此卡只作為購物優(yōu)惠憑證不能頂替貨款),花300元買這種卡后,憑卡可在這家商場按標(biāo)價(jià)的8折購物.
(1)顧客購買多少元金額的商品時(shí),買卡與不買卡花錢相等?在什么情況下購物合算?
(2)小張要買一臺(tái)標(biāo)價(jià)為3500元的冰箱,如何購買合算?小張能節(jié)省多少元錢?
(3)小張按合算的方案,把這臺(tái)冰箱買下,如果商場還能盈利25%,這臺(tái)冰箱的進(jìn)價(jià)是多少元?
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
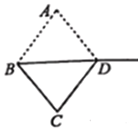
【題目】如圖,菱形紙片ABCD中,![]() ,將紙片沿對角線BD剪開,再將
,將紙片沿對角線BD剪開,再將![]() 沿射線
沿射線![]() 的方向平移得到
的方向平移得到![]() .當(dāng)
.當(dāng)![]() 是直角三角形時(shí),
是直角三角形時(shí),![]() 平移的距離為___
平移的距離為___
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】某商店銷售一種成本為20元的商品,經(jīng)調(diào)研,當(dāng)該商品每件售價(jià)為30元時(shí),每天可銷售200件:當(dāng)每件的售價(jià)每增加1元,每天的銷量將減少5件.
![]() 求銷量
求銷量![]() 件
件![]() 與售價(jià)
與售價(jià)![]() 元
元![]() 之間的函數(shù)表達(dá)式;
之間的函數(shù)表達(dá)式;
![]() 如果每天的銷量不低于150件,那么,當(dāng)售價(jià)為多少元時(shí),每天獲取的利潤最大,最大利潤是多少?
如果每天的銷量不低于150件,那么,當(dāng)售價(jià)為多少元時(shí),每天獲取的利潤最大,最大利潤是多少?
![]() 該商店老板熱心公益事業(yè),決定從每天的銷售利潤中捐出100元給希望工程,為保證捐款后每天剩余利潤不低于2900元,請直接寫出該商品售價(jià)的范圍.
該商店老板熱心公益事業(yè),決定從每天的銷售利潤中捐出100元給希望工程,為保證捐款后每天剩余利潤不低于2900元,請直接寫出該商品售價(jià)的范圍.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
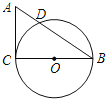
【題目】在Rt△ACB中,∠C=90°,AC=3 cm,BC=4 cm,以BC為直徑作☉O交AB于點(diǎn)D.
(1)求線段AD的長度;
(2)點(diǎn)E是線段AC上的一點(diǎn),試問當(dāng)點(diǎn)E在什么位置時(shí),直線ED與☉O相切?請說明理由.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
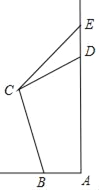
【題目】如圖,我校本部教師樓AD上有“育才中學(xué)”四個(gè)字的展示牌DE,某數(shù)學(xué)興趣小組的同學(xué)準(zhǔn)備利用所學(xué)的三角函數(shù)知識(shí)估測該教師樓的高度,由于場地有限,不便測量,所以小明沿坡度i=![]() :1的階梯從看臺(tái)前的B處前行50米到達(dá)C處,測得展示牌底部D的仰角為45°,展示牌頂部E的仰角為53°(小明的身高忽略不計(jì)),已知展示牌高DE=15米,則該教師樓AD的高度約為( )米.(參考數(shù)據(jù):Sin37°≈0,6,cos 37°≈0,8,tan37°≈0.75,
:1的階梯從看臺(tái)前的B處前行50米到達(dá)C處,測得展示牌底部D的仰角為45°,展示牌頂部E的仰角為53°(小明的身高忽略不計(jì)),已知展示牌高DE=15米,則該教師樓AD的高度約為( )米.(參考數(shù)據(jù):Sin37°≈0,6,cos 37°≈0,8,tan37°≈0.75,![]() ≈1.7)
≈1.7)
A. 102.5B. 87.5C. 85D. 70
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com