【題目】如圖，已知AB∥CD.
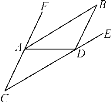
(1)判斷∠FAB與∠C的大小關系，請說明理由；
(2)若∠C＝35°，AB是∠FAD的平分線．
①求∠FAD的度數；
②若∠ADB＝110°，求∠BDE的度數．
【答案】(1)∠FAB＝∠C；(2) ①∠FAD＝70°；②∠BDE＝35°
【解析】
（1）相等，根據平行線的性質由AB∥CD，得到∠FAB=∠C即可；
（2）①根據角平分線的定義得到∠FAD=2∠FAB，代入求出即可；
②求出∠ADB+∠FAD=180°，根據平行線的判定得出CF∥BD，再根據平行線的性質推出∠BDE=∠C=35°．
（1）∠FAB與∠C的大小關系是相等，
理由是：∵AB∥CD，
∴∠FAB=∠C．
（2）①∵∠FAB=∠C=35°，
∵AB是∠FAD的平分線，
∴∠FAD=2∠FAB=2×35°=70°，
答：∠FAD的度數是70°．
②∵∠ADB=110°，∠FAD=70°，
∴∠ADB+∠FAD=110°+70°=180°，
∴CF∥BD，
∴∠BDE=∠C=35°，
答：∠BDE的度數是35°．
第1卷單元月考期中期末系列答案科目：初中數學 來源： 題型：
【題目】某校260名學生參加植樹活動，要求每人植樹4﹣7顆，活動結束后隨機抽查了20名學生每人的植樹數量，并分為四種類型，A：4顆；B：5顆；C：6顆；D：7顆．將各類的人數繪制成扇形圖（如圖1）和條形圖（如圖2），經確認扇形圖是正確的，而條形圖尚有一處錯誤．
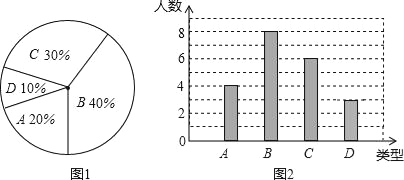
回答下列問題：
（1）寫出條形圖中存在的錯誤，并說明理由；
（2）寫出這20名學生每人植樹量的眾數和中位數；
（3）求這20名學生每人植樹量的平均數，并估計這260名學生共植樹多少棵？
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖是某月的日歷表，在此目歷表上可以用一個“十”字圈出5個數．
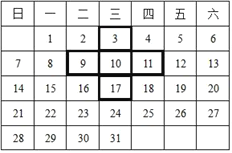
(1)如圖中四周的4個數3、9、17、11的和與中間的數10有什么數量關系？
(2)照此方法，任意圈出的5個數是否都具有這樣的數量關系？請通過整式的運算說明理由．
(3)用(2)的結論說明圈出的5個數的和能否等于125？
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】某校學生在電腦培訓前后各參加了一次水平相同的考試，考分都以同一標準劃分成“不合格”、“合格”、“優秀”三個等級．為了了解電腦培訓的效果，隨機抽取其中32名學生兩次考試考分等級制成統計圖（如圖），試回答下列問題：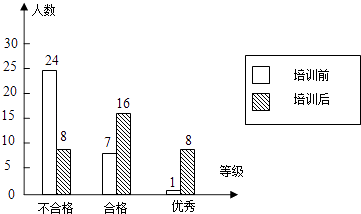 
（1）這32名學生經過培訓，考分等級“不合格”的百分比由下降到；
（2）估計該校640名學生，培訓后考分等級為“合格”與“優秀”的學生共有多少名．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，某同學在大樓AD的觀光電梯中的E點測得大樓BC樓底C點的俯角為45°，此時該同學距地面高度AE為20米，電梯再上升5米到達D點，此時測得大樓BC樓頂B點的仰角為37°，求大樓的高度BC．
（參考數據：sin37°≈0.60，cos37°≈0.80，tan37°≈0.75）．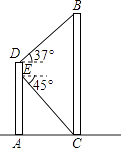
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，在平面直角坐標系中，△ABC的頂點A的坐標為（0，﹣1），頂點B在x軸的負半軸上，頂點C在y軸的正半軸上，且∠ABC＝90°，∠ACB＝30°，線段OC的垂直平分線分別交OC，BC于點D，E．
（1）點C的坐標；
（2）點P為線段ED的延長線上的一點，連接PC，PA，設點P的橫坐標為t，△ACP的面積為S，求S與t的函數關系式；
（3）在（2）的條件下，點F為線段BC的延長線上一點，連接OF，若OF＝CP，求∠OFP的度數．
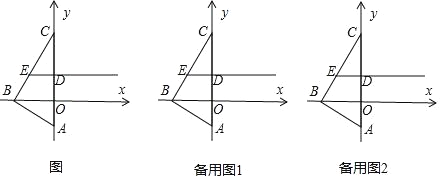
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，C為∠AOB的邊OA上一點，OC=6，N為邊OB上異于點O的一動點，P是線段CN上一點，過點P分別作PQ∥OA交OB于點Q，PM∥OB交OA于點M．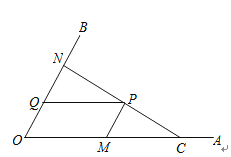
（1）若∠AOB=60°，OM=4，OQ=1，求證：CN⊥OB
（2）當點N在邊OB上運動時，四邊形OMPQ始終保持為菱形．
①問：
﹣
的值是否發生變化？如果變化，求出其取值范圍；如果不變，請說明理由．
②設菱形OMPQ的面積為S1 ， △NOC的面積為S2 ， 求
的取值范圍．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
