【題目】如圖，在
中，
，且
在
上，
于
，
交
于點
．若
，則
的度數是（ ）
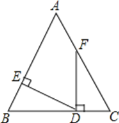
A.160°B.150°C.140°D.120°
【答案】A
【解析】
由DF⊥BC有∠FDB=90°，而∠EDF=70°，根據由∠BDE=∠FDB-∠EDF可求得∠BDE的度數，由DE⊥AB得到∠DEB=90°，根據三角形內角和定理得到求出∠B的度數和∠C的度數，進而求出∠CFD的度數，利用鄰補角的知識求出∠AFD的度數．
解：∵DF⊥BC，
∴∠FDB=90°，
而∠EDF=70°，
∴∠BDE=∠FDB-∠EDF=90°-70°=20°，
∵DE⊥AB，
∴∠DEB=90°，
∴∠B=180°-∠DEB-∠BDE=180°-90°-20°=70°，
又∵AB=AC，
∴∠C=∠B=70°，
∴∠CFD=90°-70°=20°，
∴∠AFD=180°-20°=160°．
故選：A．
習題精選系列答案科目：初中數學 來源： 題型：
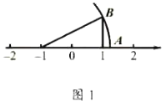
【題目】（1）如圖1，
中，
，點
在數軸-1處，點
在數軸1處，
，
，則數軸上點
對應的數是 ．
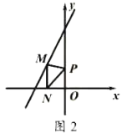
（2）如圖2，點是直線
上的動點，過點作
垂直
軸于點
，點
是
軸上的動點，當以，，為頂點的三角形為等腰直角三角形時點的坐標為 ．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，已知直線y＝
x與雙曲線y＝
交于A、B兩點，且點A的橫坐標為
．
（1）求k的值；
（2）若雙曲線y＝上點C的縱坐標為3，求△AOC的面積；
（3）在坐標軸上有一點M，在直線AB上有一點P，在雙曲線y＝上有一點N，若以O、M、P、N為頂點的四邊形是有一組對角為60°的菱形，請寫出所有滿足條件的點P的坐標．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】為了爭創全國文明衛生城市，優化城市環境，節約能源，某市公交公司決定購買一批共10臺全新的混合動力公交車，現有A、B兩種型號，其中每臺的價格，年省油量如下表：
A | B | |
價格（萬元／臺） | a | b |
節省的油量（萬升／年） | 2.4 | 2 |
經調查，購買一臺A型車比購買一臺B型車多10萬元，購買3臺A型車比購買4臺B型車少30萬元．
（1）請求出a和b的值；
（2）若購買這批混合動力公交車（兩種車型都要有）每年能節省的油量不低于21.6萬升，請問有幾種購車方案？請寫出解答過程．
（3）求（2）中最省錢的購車方案及所需的購車款．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，在等腰△ABC中，AB＝AC，∠BAC＝50°．∠BAC的平分線與AB的中垂線交于點O，點C沿EF折疊后與點O重合，則∠CEF的度數是 ．
查看答案和解析>>
科目：初中數學 來源： 題型：
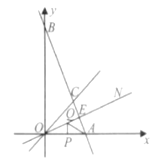
【題目】如下圖，在平面直角坐標系中，直線AB與x軸交于點A,與y軸交于點B，與直線OC:y=x交于點C.
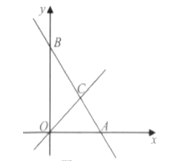
(1)若直線AB解析式為
.
①求點C的坐標；
②根據圖象，求關于x的不等式0<-
x+10<x的解集；
(2)如下圖，作∠AOC的平分線ON,若AB⊥ON,垂足為E,ΔOAC的面積為9，且OA=6，P、Q分別為線段OA、OE上的動點，連接AQ與PQ,試探索AQ+PQ是否存在最小值?若存在，求出這個最小值:若不存在，說明理由.
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖1，△ABC中，AD是∠BAC的角平分線，若AB=AC+CD.那么∠ACB 與∠ABC有怎樣的數量關系? 小明通過觀察分析，形成了如下解題思路:
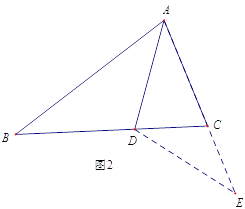
如圖2,延長AC到E,使CE=CD,連接DE,由AB=AC+CD,可得AE=AB,又因為AD是∠BAC的平分線，可得△ABD≌△AED,進一步分析就可以得到∠ACB 與∠ABC的數量關系.
(1) 判定△ABD 與△AED 全等的依據是______________(SSS,SAS,ASA,AAS 從其中選擇一個);
(2)∠ACB 與∠ABC的數量關系為:___________________
查看答案和解析>>
科目：初中數學 來源： 題型：
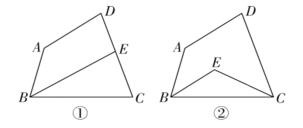
【題目】如圖，在四邊形ABCD中，∠A＝140°，∠D＝80°．
（1）如圖①，若∠ABC的平分線BE交DC于點E，且BE∥AD，試求出∠C的度數；
（2）如圖②，若∠ABC和∠BCD的平分線交于點E，試求出∠BEC的度數．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
