
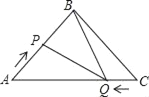
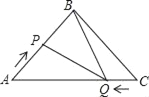
【題目】如圖,在![]() 中,
中,![]() ,
,![]() ,點
,點![]() 從
從![]() 點出發(fā),沿著
點出發(fā),沿著![]() 以每秒
以每秒![]() 的速度向
的速度向![]() 點運動;同時點
點運動;同時點![]() 從
從![]() 點出發(fā),沿
點出發(fā),沿![]() 以每秒
以每秒![]() 的速度向
的速度向![]() 點運動,設(shè)運動時間為
點運動,設(shè)運動時間為![]() 秒.
秒.
(1)當(dāng)![]() 為何值時,
為何值時,![]() ;
;
(2)是否存在某一時刻,使![]() ?若存在,求出此時
?若存在,求出此時![]() 的長;若不存在,請說理由;
的長;若不存在,請說理由;
(3)當(dāng)![]() 時,求
時,求![]() 的值.
的值.
【答案】(1)當(dāng)x=![]() 時,PQ∥BC;(2)存在,AP=
時,PQ∥BC;(2)存在,AP=![]() ;(3)
;(3)![]() =
=![]() .
.
【解析】
(1)由PQ∥BC,得出比例式![]() ,即可求出x的值;
,即可求出x的值;
(2)由BA=BC得∠A=∠C.要使△APQ∽△CQB,只需![]() ,此時
,此時![]() 解這個方程就可解決問題.
解這個方程就可解決問題.
(3)當(dāng)CQ=10時,可求出x,從而求出AP,即可求出BP,然后根據(jù)兩個三角形兩底上的高相等時,這兩個三角形的面積比等于這兩個底的比,就可解決問題;
解:(1)由題可得AP=4x,CQ=3x.
∵BA=BC=20,AC=30,
∴BP=20﹣4x,AQ=30﹣3x.
若PQ∥BC,
則有△APQ∽△ABC,
∴![]()
∴![]()
解得:x=![]() .
.
∴當(dāng)x=![]() 時,PQ∥BC;
時,PQ∥BC;
(2)存在.
∵BA=BC,∴∠A=∠C.
要使△APQ∽△CQB,
只需![]()
此時![]()
解得:x=![]() ,
,
∴AP=4x=![]() ;
;
(3)當(dāng)CQ=10時,3x=10,
∴x=![]() ,
,
∴AP=4x=![]() ,
,
∴![]()


 名校課堂系列答案
名校課堂系列答案科目:初中數(shù)學(xué) 來源: 題型:
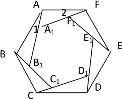
【題目】如圖的花環(huán)狀圖案中,ABCDEF和A1B1C1D1E1F1都是正六邊形.
(1)求證:∠1=∠2;
(2)找出一對全等的三角形并給予證明.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,在平面直角坐標(biāo)系![]() 中,正方形ABCO的對角線BO在x 軸上,若正方形ABCO的邊長為
中,正方形ABCO的對角線BO在x 軸上,若正方形ABCO的邊長為![]() ,點B在x負半軸上,反比例函數(shù)
,點B在x負半軸上,反比例函數(shù)![]() 的圖象經(jīng)過C點.
的圖象經(jīng)過C點.
(1)求該反比例函數(shù)的解析式;
(2)當(dāng)函數(shù)值![]() >-2時,請直接寫出自變量x的取值范圍;
>-2時,請直接寫出自變量x的取值范圍;
(3)若點P是反比例函數(shù)上的一點,且△PBO的面積恰好等于正方形ABCO的面積,求點P的坐標(biāo).

查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
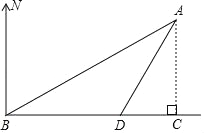
【題目】如圖,海中有一小島A,它周圍8海里內(nèi)有暗礁,漁船由西向東航行,在B點測得小島A在北偏東60°方向上,航行12海里到達D點,這時測得小島A在北偏東30°方向上.
(1)求∠BAD的度數(shù);
(2)如果漁船不改變航線繼續(xù)向東航行,有沒有觸礁的危險?
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】《如果想毀掉一個孩子,就給他一部手機!》這是2017年微信圈一篇熱傳的文章.國際上,法國教育部宣布從 2018 年9月新學(xué)期起小學(xué)和初中禁止學(xué)生使用手機.為了解學(xué)生手機使用情況,某學(xué)校開展了“手機伴我健康行”主題活動,他們隨機抽取部分學(xué)生進行“使用手機目的”和“每周使用手機的時間”的問卷調(diào)查,并繪制成如圖①,②的 統(tǒng)計圖,已知“查資料”的人數(shù)是 40人.請你根據(jù)以上信息解答下列問題:
(1)在扇形統(tǒng)計圖中,“玩游戲”對應(yīng)的百分比為______,圓心角度數(shù)是______度;
(2)補全條形統(tǒng)計圖;
(3)該校共有學(xué)生2100人,估計每周使用手機時間在2 小時以上(不含2小時)的人數(shù).
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,在平面直角坐標(biāo)系![]() 中,一次函數(shù)
中,一次函數(shù)![]() (a為常數(shù))的圖象與y軸相交于點A,與函數(shù)
(a為常數(shù))的圖象與y軸相交于點A,與函數(shù)![]() (x>0)的圖象相交于點B(m,1).
(x>0)的圖象相交于點B(m,1).
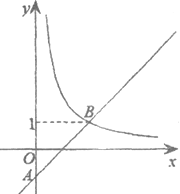
(1)求點B的坐標(biāo)及一次函數(shù)的解析式;
(2)若點P在y軸上,且△PAB為直角三角形,請直接寫出點P的坐標(biāo).
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】點A(x1,y1)、B(x2,y2)都在某函數(shù)圖象上,且當(dāng)x1<x2<0時,y1>y2,則此函數(shù)一定不是( )
A. ![]() B. y=﹣2x+1 C. y=x2﹣1 D.
B. y=﹣2x+1 C. y=x2﹣1 D. ![]()
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
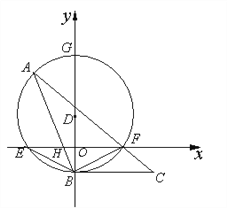
【題目】如圖,在平面直角坐標(biāo)中,點D在y軸上,以D為圓心,作⊙D交x軸于點E、F,交y軸于點B、G,點A在![]() 上,連接AB交x軸于點H,連接 AF并延長到點C,使∠FBC=∠A.
上,連接AB交x軸于點H,連接 AF并延長到點C,使∠FBC=∠A.
(1)判斷直線BC與⊙D的位置關(guān)系,并說明理由;
(2)求證:BE2=BH·AB;
(3) 若點E坐標(biāo)為(-4,0),點B的坐標(biāo)為(0,-2),AB=8,求F與A兩點的坐標(biāo).
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,已知拋物線y=﹣x2+bx+c與一直線相交于A(1,0)、C(﹣2,3)兩點,與y軸交于點N,其頂點為D.
(1)求拋物線及直線AC的函數(shù)關(guān)系式;
(2)若P是拋物線上位于直線AC上方的一個動點,求△APC的面積的最大值及此時點P的坐標(biāo);
(3)在對稱軸上是否存在一點M,使△ANM的周長最小.若存在,請求出M點的坐標(biāo)和△ANM周長的最小值;若不存在,請說明理由.

查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com