
【題目】已知:如圖所示,在△ABC中,∠B=90°,AB=5cm,BC=7cm,點P從點A開始沿AB邊向點B以1cm/s的速度移動,點Q從點B開始沿BC邊向點C以2cm/s的速度移動.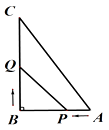
(1)如果P,Q分別從A,B同時出發,那么幾秒后,△PBQ的面積等于4cm2?
(2)如果P,Q分別從A,B同時出發,那么幾秒后,△PBQ中PQ的長度等于5cm?
(3)在(1)中,當P,Q出發幾秒時,△PBQ有最大面積?
【答案】
(1)解:設t秒后,△PBQ的面積等于4cm2 ,
則列方程為:(5-t)×2t× ![]() =4,
=4,
解得t1=1,t2=4(舍),
答:1秒后,△PBQ的面積等于4cm2.
(2)解:設x秒后,△PBQ中PQ的長度等于5cm,
列方程為:(5-x)2+(2x)2=52 ,
解得x1=0(舍),x2=2,
答:2秒后,△PBQ中PQ的長度等于5cm。
(3)解:設面積為Scm2 , 時間為t,
則S=(5-t)×2t× ![]() =-t2+5t,
=-t2+5t,
當t=2.5時,面積最大.
【解析】(1)設t秒后,△PBQ的面積等于4cm2 , 根據題意PA=t ,BP=5-t ,BQ=2t ,根據三角形的面積公式及三角形的面積等于4,列出方程,求解并檢驗即可;
(2)設x秒后,△PBQ中PQ的長度等于5cm,根據題意PA=x ,BP=5-tx,BQ=2x ,根據勾股定理得出方程,求解并檢驗即可;
(3)設面積為Scm2 , 時間為t,根據三角形的面積公式得出S與t的函數解析式,從而得出次函數是S與t的二次函數,然后利用頂點坐標公式得出當t=2.5時,面積最大.


 新編小學單元自測題系列答案
新編小學單元自測題系列答案 字詞句段篇系列答案
字詞句段篇系列答案科目:初中數學 來源: 題型:
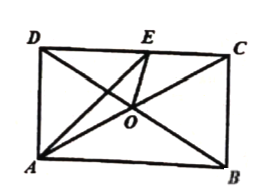
【題目】如圖,在矩形![]() 中,
中,![]() 平分
平分![]() 交
交![]() 于點
于點![]() ,給出以下結論:①
,給出以下結論:①![]() 為等腰直角三角形;②
為等腰直角三角形;②![]() 為等邊三角形;③
為等邊三角形;③![]() ;④
;④![]() ⑤
⑤![]() 是
是![]() 的中位線.其中正確的結論有( )
的中位線.其中正確的結論有( )
A.![]() 個B.
個B.![]() 個C.
個C.![]() 個D.
個D.![]() 個
個
查看答案和解析>>
科目:初中數學 來源: 題型:
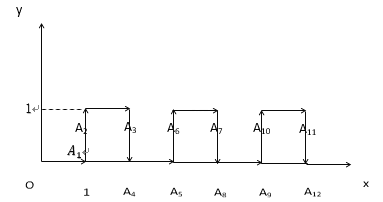
【題目】在平面直角坐標系中,一個智能機器人接到如下指令,從原點O出發,按向右、向上、向右、向下的方向依次不斷移動,每次移動1個單位長度,其行走的路線如圖所示,第1次移動到A1,第2次移動到A2……,第n次移動到An,則三角形OA2A2018的面積是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
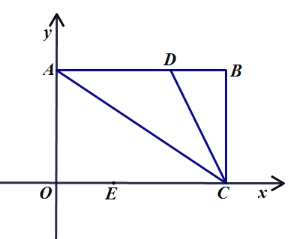
【題目】如圖1,把矩形![]() 放在平面直角坐標系中,邊
放在平面直角坐標系中,邊![]() 在
在![]() 軸上,邊
軸上,邊![]() 在
在![]() 軸上,連接
軸上,連接![]() ,且
,且![]() ,過點
,過點![]() 作
作![]() 平分
平分![]() 交
交![]() 于點
于點![]() .動點
.動點![]() 在線段
在線段![]() 上運動,過
上運動,過![]() 作
作![]() 交
交![]() 于
于![]() ,過
,過![]() 作
作![]() 交
交![]() 于
于![]() .
.
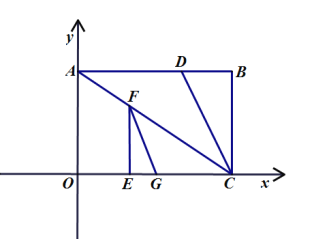
(1)當![]() 時,在線段
時,在線段![]() 上有一動點
上有一動點![]() ,
,![]() 軸上有一動點
軸上有一動點![]() ,連接
,連接![]() 當
當![]() 周長最小時,求
周長最小時,求![]() 周長的最小值及此時點
周長的最小值及此時點![]() 的坐標;
的坐標;
(2)如圖2,在(1)問的條件下,點![]() 是直線
是直線![]() 上的一個動點,問:在
上的一個動點,問:在![]() 軸上是否存在
軸上是否存在![]() 點,使得
點,使得![]() 是以
是以![]() 為腰的等腰直角三角形?若存在,請直接寫出
為腰的等腰直角三角形?若存在,請直接寫出![]() 點及對應的
點及對應的![]() 點的坐標,若沒有,請說明理由.
點的坐標,若沒有,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在矩形ABCD中,E、F分別是邊AB、CD上的點,AE=CF,連接EF,BF,EF與對角線AC交于O點,且BE=BF,∠BEF=2∠BAC。

(1)求證:OE=OF;
(2)若BC=![]() ,求AB的長。
,求AB的長。
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖1,直線MN與直線AB、CD分別交于點E、F,∠1與∠2互補.
(1)試判斷直線AB與直線CD的位置關系,并說明理由;
(2)如圖2,∠BEF與∠EFD的角平分線交于點P,EP與CD交于點G,點H是MN上一點,且GH⊥EG,求證:PF∥GH;
(3)如圖3,在(2)的條件下,連接PH,K是GH上一點使∠PHK=∠HPK,作PQ平分∠EPK,問∠HPQ的大小是否發生變化?若不變,請求出其值;若變化,說明理由.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,菱形OABC的一邊OA在x軸的負半軸上,O是坐標原點,tan∠AOC= ![]() ,反比例函數y=
,反比例函數y= ![]() 的圖象經過點C,與AB交于點D,若△COD的面積為20,則k的值等于 .
的圖象經過點C,與AB交于點D,若△COD的面積為20,則k的值等于 . 
查看答案和解析>>
科目:初中數學 來源: 題型:
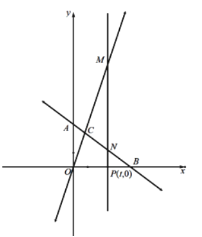
【題目】在平面直角坐標系之中,點O為坐標原點,直線![]() 分別交x、y軸于點B、A,直線
分別交x、y軸于點B、A,直線![]() 與直線
與直線![]() 交于點C.
交于點C.
(1)如圖1,求點C的坐標.
(2)如圖2,點P(t,0)為C點的右側x軸上一點,過點P作x軸垂線分別交AB、OC于點N、M,若MN=5NP,求t的值.
(3)如圖3,點F為平面內任意一點,是否存在y軸正半軸上一點E,使點E、F、M、N圍成的四邊形為菱形,若存在求出點E坐標;若不存在,請說明理由.



查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com