
【題目】已知:在![]() 中,C、D分別為BM、AM上的點(diǎn),四邊形ABCD內(nèi)接于
中,C、D分別為BM、AM上的點(diǎn),四邊形ABCD內(nèi)接于![]() ,連接AC,
,連接AC,![]() ;
;
![]() 如圖
如圖![]() ,求證:弧
,求證:弧![]() 弧BD;
弧BD;
![]() 如圖
如圖![]() ,若AB為直徑,
,若AB為直徑,![]() ,求
,求![]() 值;
值;
![]() 如圖
如圖![]() ,在
,在![]() 的條件下,E為弧CD上一點(diǎn)
的條件下,E為弧CD上一點(diǎn)![]() 不與C、D重合
不與C、D重合![]() ,F為AB上一點(diǎn),連接EF交AC于點(diǎn)N,連接DN、DE,若
,F為AB上一點(diǎn),連接EF交AC于點(diǎn)N,連接DN、DE,若![]() ,
,![]() ,
,![]() ,求AN的長(zhǎng).
,求AN的長(zhǎng).
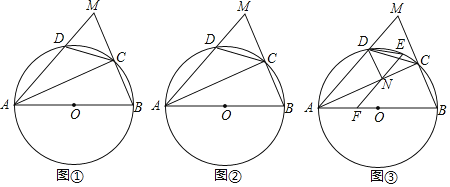
【答案】(1)詳見解析;(2)![]() (3)
(3)![]()
【解析】
![]() 證明弧
證明弧![]() 弧BD可以轉(zhuǎn)化證明
弧BD可以轉(zhuǎn)化證明![]()
![]() 是直徑可知三角形ABD是等腰直角三角形,從而得出
是直徑可知三角形ABD是等腰直角三角形,從而得出![]() ,利用
,利用![]() 的特殊性構(gòu)造直角三角形DCG,結(jié)合
的特殊性構(gòu)造直角三角形DCG,結(jié)合![]() ,可以求出
,可以求出![]() ,進(jìn)而求出
,進(jìn)而求出![]()
![]() 為了求AN,可以過點(diǎn)N作
為了求AN,可以過點(diǎn)N作![]() 于點(diǎn)M,求出MN,AM,即可求出
于點(diǎn)M,求出MN,AM,即可求出![]() 因?yàn)?/span>P是BD的中點(diǎn),所以連結(jié)OP,根據(jù)垂徑定理可以得出
因?yàn)?/span>P是BD的中點(diǎn),所以連結(jié)OP,根據(jù)垂徑定理可以得出![]() ,根據(jù)
,根據(jù)![]() 可得
可得![]() ,從而得到矩形OPLH,結(jié)合矩形的性質(zhì),可以得出OH,EH的長(zhǎng)度關(guān)系,在利用勾股定理建立方程,可求出HO,進(jìn)而求出MN,AM,最終得出AN的長(zhǎng)度.
,從而得到矩形OPLH,結(jié)合矩形的性質(zhì),可以得出OH,EH的長(zhǎng)度關(guān)系,在利用勾股定理建立方程,可求出HO,進(jìn)而求出MN,AM,最終得出AN的長(zhǎng)度.
![]() ,
,![]()
![]() ,
,
又![]()
![]() ,
,
![]() 弧
弧![]() 弧BD
弧BD
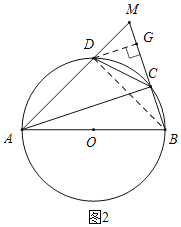
![]() 作
作![]() 于點(diǎn)G,連結(jié)
于點(diǎn)G,連結(jié)![]() 如圖
如圖![]()
![]() 為直徑
為直徑
弧![]() 弧
弧![]()
![]() ,
,
又![]()
![]() ,
,
又![]()
![]() ,
,
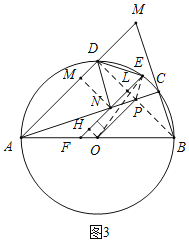
![]() 連結(jié)BD交AC,EF分別為點(diǎn)P,點(diǎn)L,連結(jié)OP,OE,PE,再作
連結(jié)BD交AC,EF分別為點(diǎn)P,點(diǎn)L,連結(jié)OP,OE,PE,再作![]() 于點(diǎn)H,
于點(diǎn)H,![]() 于點(diǎn)
于點(diǎn)![]() 如圖3所示
如圖3所示![]()
![]() ,
,![]() ,
,
![]() ,
,
由![]() 得
得![]()
![]() ,
,
即P為BD的中點(diǎn)
![]() ,
,
![]() 四邊形OPLH為矩形
四邊形OPLH為矩形
設(shè)![]() ,則
,則![]() .
.
又![]()
![]() 垂直平分NE
垂直平分NE
![]() ,
,
又![]() 為等腰直角三角形
為等腰直角三角形
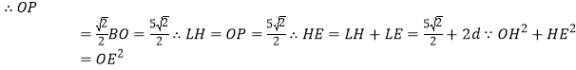
![]() ,
,
解得![]()
![]() ,
,
![]() .
.


 品學(xué)雙優(yōu)卷系列答案
品學(xué)雙優(yōu)卷系列答案 小學(xué)期末沖刺100分系列答案
小學(xué)期末沖刺100分系列答案 期末復(fù)習(xí)檢測(cè)系列答案
期末復(fù)習(xí)檢測(cè)系列答案 超能學(xué)典單元期中期末專題沖刺100分系列答案
超能學(xué)典單元期中期末專題沖刺100分系列答案
| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,點(diǎn)![]() 都在反比例函數(shù)
都在反比例函數(shù)![]() 的圖象上.
的圖象上.
(1)求![]() 的值;
的值;
(2)如果![]() 為
為![]() 軸上一點(diǎn),
軸上一點(diǎn),![]() 為
為![]() 軸上一點(diǎn),以點(diǎn)
軸上一點(diǎn),以點(diǎn)![]() 為頂點(diǎn)的四邊形是平行四邊形,試求直線
為頂點(diǎn)的四邊形是平行四邊形,試求直線![]() 的函數(shù)表達(dá)式;
的函數(shù)表達(dá)式;
(3)將線段![]() 沿直線
沿直線![]() 進(jìn)行對(duì)折得到線段
進(jìn)行對(duì)折得到線段![]() ,且點(diǎn)
,且點(diǎn)![]() 始終在直線
始終在直線![]() 上,當(dāng)線段
上,當(dāng)線段![]() 與
與![]() 軸有交點(diǎn)時(shí),則
軸有交點(diǎn)時(shí),則![]() 的取值范圍為_______(直接寫出答案)
的取值范圍為_______(直接寫出答案)

查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
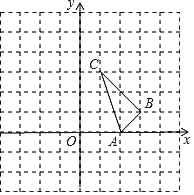
【題目】如圖,在平面直角坐標(biāo)系中,已知A(2,0)、B(3,1)、C(1,3).
(1)將△ABC沿x軸負(fù)方向移動(dòng)2個(gè)單位長(zhǎng)度至△A1B1C1,畫圖并寫出點(diǎn)C1的坐標(biāo);
(2)以點(diǎn)A1為旋轉(zhuǎn)中心,將△A1B1C1逆時(shí)針方向旋轉(zhuǎn)90°得到△A2B2C2,畫圖并寫出點(diǎn)C2的坐標(biāo);
(3)以B、C1、C2為頂點(diǎn)的三角形是 三角形,其外接圓的半徑R= .
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】為滿足市場(chǎng)需求,某超市在五月初五“端午節(jié)”來臨前夕,購(gòu)進(jìn)一種品牌粽子,每盒進(jìn)價(jià)是40元.超市規(guī)定每盒售價(jià)不得少于45元.根據(jù)以往銷售經(jīng)驗(yàn)發(fā)現(xiàn);當(dāng)售價(jià)定為每盒45元時(shí),每天可以賣出700盒,每盒售價(jià)每提高1元,每天要少賣出20盒.
(1)試求出每天的銷售量y(盒)與每盒售價(jià)x(元)之間的函數(shù)關(guān)系式;
(2)當(dāng)每盒售價(jià)定為多少元時(shí),每天銷售的利潤(rùn)P(元)最大?最大利潤(rùn)是多少?
(3)為穩(wěn)定物價(jià),有關(guān)管理部門限定:這種粽子的每盒售價(jià)不得高于58元.如果超市想要每天獲得不低于6000元的利潤(rùn),那么超市每天至少銷售粽子多少盒?
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】為滿足市場(chǎng)需求,某超市在五月初五“端午節(jié)”來臨前夕,購(gòu)進(jìn)一種品牌粽子,每盒進(jìn)價(jià)是40元.超市規(guī)定每盒售價(jià)不得少于45元.根據(jù)以往銷售經(jīng)驗(yàn)發(fā)現(xiàn);當(dāng)售價(jià)定為每盒45元時(shí),每天可以賣出700盒,每盒售價(jià)每提高1元,每天要少賣出20盒.
(1)試求出每天的銷售量y(盒)與每盒售價(jià)x(元)之間的函數(shù)關(guān)系式;
(2)當(dāng)每盒售價(jià)定為多少元時(shí),每天銷售的利潤(rùn)P(元)最大?最大利潤(rùn)是多少?
(3)為穩(wěn)定物價(jià),有關(guān)管理部門限定:這種粽子的每盒售價(jià)不得高于58元.如果超市想要每天獲得不低于6000元的利潤(rùn),那么超市每天至少銷售粽子多少盒?
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖是二次函數(shù)![]() (a、b、c是常數(shù),a≠0)圖象的一部分,與x軸的交點(diǎn)A在點(diǎn)(2,0)和(3,0)之間,對(duì)稱軸是x=1.對(duì)于下列說法:①當(dāng)
(a、b、c是常數(shù),a≠0)圖象的一部分,與x軸的交點(diǎn)A在點(diǎn)(2,0)和(3,0)之間,對(duì)稱軸是x=1.對(duì)于下列說法:①當(dāng)![]() 時(shí),
時(shí),![]() ;②
;②![]() ;③
;③![]() ;④3a+c>0,其中正確的是( )
;④3a+c>0,其中正確的是( )
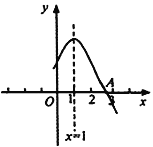
A. ①③B. ①④C. ②③D. ②④
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
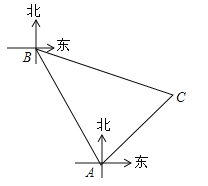
【題目】(6分)某海域有A,B兩個(gè)港口,B港口在A港口北偏西30°方向上,距A港口60海里,有一艘船從A港口出發(fā),沿東北方向行駛一段距離后,到達(dá)位于B港口南偏東75°方向的C處,求該船與B港口之間的距離即CB的長(zhǎng)(結(jié)果保留根號(hào)).
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
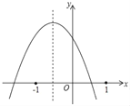
【題目】已知:二次函數(shù)y=ax2+bx+c的圖象如圖所示,下列結(jié)論中:
①abc<0;②b2﹣4ac>0;③3a+c<0;④(a+c)2<b2,⑤a+b+c>0
其中正確的序號(hào)是_____.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
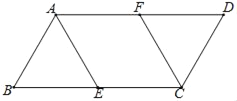
【題目】如圖,在平行四邊形ABCD中,![]() ,點(diǎn)E、F分別是BC、AD的中點(diǎn).
,點(diǎn)E、F分別是BC、AD的中點(diǎn).
(1)求證:![]() ≌
≌![]() ;
;
(2)當(dāng)![]() 時(shí),求四邊形AECF的面積.
時(shí),求四邊形AECF的面積.
查看答案和解析>>
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com