
【題目】(感知)如圖①在等邊△ABC和等邊△ADE中,連接BD,CE,易證:△ABD≌△ACE;
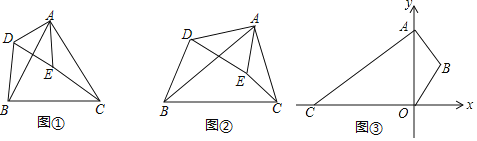
(探究)如圖②△ABC與△ADE中,∠BAC=∠DAE,∠ABC=∠ADE,求證:△ABD∽△ACE;
(應用)如圖③,點A的坐標為(0,6),AB=BO,∠ABO=120°,點C在x軸上運動,在坐標平面內作點D,使AD=CD,∠ADC=120°,連結OD,則OD的最小值為 .
【答案】探究:見解析;應用:![]() .
.
【解析】
探究:由△DAE∽△BAC,推出![]() ,可得
,可得![]() ,由此即可解決問題;
,由此即可解決問題;
應用:當點D在AC的下方時,先判定△ABO∽△ADC,得出![]() ,再根據∠BAD=∠OAC,得出△ACO∽△ADB,進而得到∠ABD=∠AOC=90°,得到當OD⊥BE時,OD最小,最后過O作OF⊥BD于F,根據∠OBF=30°,求得OF=
,再根據∠BAD=∠OAC,得出△ACO∽△ADB,進而得到∠ABD=∠AOC=90°,得到當OD⊥BE時,OD最小,最后過O作OF⊥BD于F,根據∠OBF=30°,求得OF=![]() OB=
OB=![]() ,即OD最小值為
,即OD最小值為![]() ;當點D在AC的上方時,作B關于y軸的對稱點B',則同理可得OD最小值為
;當點D在AC的上方時,作B關于y軸的對稱點B',則同理可得OD最小值為![]() .
.
解:探究:如圖②中,
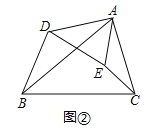
∵∠BAC=∠DAE,∠ABC=∠ADE,
∴△DAE∽△BAC,∠DAB=∠EAC,
∴![]() ,
,
∴![]() ,
,
∴△ABD∽△ACE;
應用:①當點D在AC的下方時,如圖③1中,
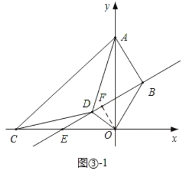
作直線BD,由∠DAC=∠DCA=∠BAO=∠BOA=30°,可得△ABO∽△ADC,
∴![]() ,即
,即![]() ,
,
又∵∠BAD=∠OAC,
∴△ACO∽△ADB,
∴∠ABD=∠AOC=90°,
∵當OD⊥BE時,OD最小,
過O作OF⊥BD于F,則△BOF為直角三角形,
∵A點的坐標是(0,6),AB=BO,∠ABO=120°,
∴易得OB=2![]() ,
,
∵∠ABO=120°,∠ABD=90°,
∴∠OBF=30°,
∴OF=![]() OB=
OB=![]() ,
,
即OD最小值為![]() ;
;
當點D在AC的上方時,如圖③2中,
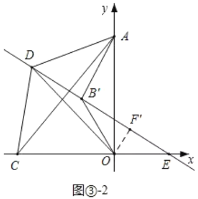
作B關于y軸的對稱點B',作直線DB',則同理可得:△ACO∽△ADB',
∴∠AB'D=∠AOC=90°,
∴當OD⊥B'E時,OD最小,
過O作OF'⊥B'D于F',則△B'OF'為直角三角形,
∵A點的坐標是(0,6),AB'=B'O,∠AB'O=120°,
∴易得OB'=2![]() ,
,
∵∠AB'O=120°,∠AB'D=90°,
∴∠OB'F'=30°,
∴OF'=![]() OB'=
OB'=![]() ,
,
即OD最小值為![]() .
.
故答案為:![]() .
.


科目:初中數學 來源: 題型:
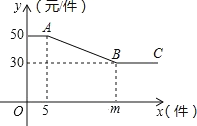
【題目】某商店經銷某種玩具,該玩具每個進價 20 元,為進行促銷,商店制定如下“優惠” 方案:如果一次銷售數量不超過 5 個,則每個按 50 元銷售:如果一次銷售數量超過 5 個,則每增加一個,所有玩具均降低 1 元銷售,但單價不得低于 30 元,一次銷售該玩具的單價 y(元)與銷售數量 x(個)之間的函數關系如下圖所示.
(1)結合圖形,求出 m 的值;射線 BC 所表示的實際意義是什么;
(2)求線段 AB 滿足的 y 與 x 之間的函數解析式,并直接寫出自變量的取值范圍;
(3)當銷售 15 個時,商店的利潤是多少元.
查看答案和解析>>
科目:初中數學 來源: 題型:
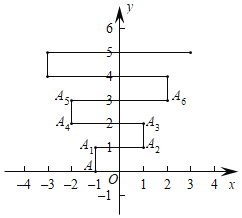
【題目】如圖,在平面直角坐標系上有個點A(﹣1,0),點A第1次向上跳動1個單位至點A1(﹣1,1),緊接著第2次向右跳動2個單位至點A2(1,1),第3次向上跳動1個單位至點A3,第4次向左跳動3個單位至點A4,第5次又向上跳動1個單位至點A5,第6次向右跳動4個單位至點A6,……,依此規律跳動下去,點A第2019次跳動至點A2019的坐標是____.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在△ABC中,AB=AC,D為BC中點,AE∥BD,且AE=BD.
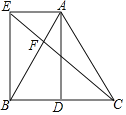
(1)求證:四邊形AEBD是矩形;
(2)連接CE交AB于點F,若BE=2![]() ,AE=2,求EF的長.
,AE=2,求EF的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】閱讀材料,并回答下列問題
如圖1,以AB為軸,把△ABC翻折180°,可以變換到△ABD的位置;
如圖2,把△ABC沿射線AC平移,可以變換到△DEF的位置.像這樣,其中的一個三角形是另一個三角形經翻折、平移等方法變換成的,這種只改變位置,不改變形狀大小的圖形變換,叫三角形的全等變換.班里學習小組針對三角形的全等變換進行了探究和討論
(1)請你寫出一種全等變換的方法(除翻折、平移外), .
(2)如圖2,前進小組把△ABC沿射線AC平移到△DEF,若平移的距離為2,且AC=5,則DC= .
(3)如圖3,圓夢小組展開了探索活動,把△ABC紙片沿DE折疊,使點A落在四邊形BCDE內部點A′的位置,且得出一個結論:2∠A′=∠1+∠2.請你對這個結論給出證明.
(4)如圖4,奮進小組則提出,如果把△ABC紙片沿DE折疊,使點A落在四邊形BCDE外部點A′的位置,此時∠A′與∠1、∠2之間結論還成立嗎?若成立,請給出證明,若不成立,寫出正確結論并證明.

查看答案和解析>>
科目:初中數學 來源: 題型:
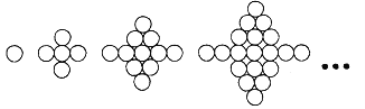
【題目】如圖,由等圓組成的一組圖中,第![]() 個圖由
個圖由![]() 個圓組成,第
個圓組成,第![]() 個圖由
個圖由![]() 個圓組成,第
個圓組成,第![]() 個圖由
個圖由![]() 個圓組成,……,按照這樣的規律排列下去,則第
個圓組成,……,按照這樣的規律排列下去,則第![]() 個圖形由______個圓組成,第
個圖形由______個圓組成,第![]() 個圖形由_____個圓組成.
個圖形由_____個圓組成.
查看答案和解析>>
科目:初中數學 來源: 題型:
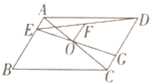
【題目】如圖,平行四邊形ABCD中,點O是對角線AC的中點,點E在邊AB上,連接DE,取DE的中點F,連接EO并延長交CD于點G.若BE=3CG,OF=2,則線段AE的長是_____.
查看答案和解析>>
科目:初中數學 來源: 題型:
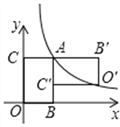
【題目】如圖,矩形![]() 的頂點
的頂點![]() 在坐標原點,頂點
在坐標原點,頂點![]() 、
、![]() 分別在
分別在![]() 、
、![]() 軸的正半軸上,頂點
軸的正半軸上,頂點![]() 在反比例函數
在反比例函數![]() (
(![]() 為常數,
為常數,![]() ,
,![]() )的圖象上,將矩形
)的圖象上,將矩形![]() 繞點
繞點![]() 按逆時針方向旋轉
按逆時針方向旋轉![]() 得到矩形
得到矩形![]() ,若點
,若點![]() 的對應點
的對應點![]() 恰好落在此反比例函數圖象上,則
恰好落在此反比例函數圖象上,則![]() 的值是__________.
的值是__________.
查看答案和解析>>
科目:初中數學 來源: 題型:
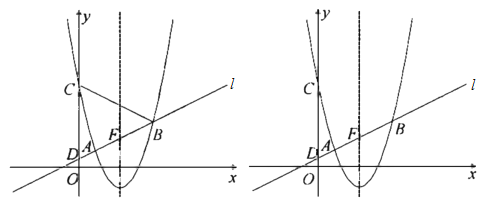
【題目】如圖,在平面直角坐標系![]() 中,以直線
中,以直線![]() 為對稱軸的拋物線
為對稱軸的拋物線![]() 與直線
與直線![]() 交于
交于![]() ,
,![]() 兩點,與
兩點,與![]() 軸交于
軸交于![]() ,直線
,直線![]() 與
與![]() 軸交于點
軸交于點![]() .
.
(1)求拋物線的函數表達式;
(2)設直線![]() 與拋物線的對稱軸的交點為
與拋物線的對稱軸的交點為![]() ,
,![]() 是拋物線上位于對稱軸右側的一點,若
是拋物線上位于對稱軸右側的一點,若![]() ,且
,且![]() 與
與![]() 的面積相等,求點
的面積相等,求點![]() 的坐標;
的坐標;
(3)若在![]() 軸上有且只有一點
軸上有且只有一點![]() ,使
,使![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com