
【題目】如圖,菱形![]() 頂點(diǎn)
頂點(diǎn)![]() 在函數(shù)
在函數(shù)![]()
![]() 的圖象上,函數(shù)
的圖象上,函數(shù)![]()
![]() 的圖象關(guān)于直線
的圖象關(guān)于直線![]() 對稱,且經(jīng)過點(diǎn)
對稱,且經(jīng)過點(diǎn)![]() ,
,![]() 兩點(diǎn),若
兩點(diǎn),若![]() ,
,![]() ,則
,則![]() 的值為________.
的值為________.

【答案】![]()
【解析】
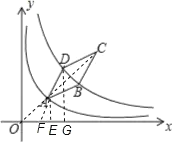
連接OC,AC過A作AE⊥x軸于點(diǎn)E,延長DA與x軸交于點(diǎn)F,過點(diǎn)D作DG⊥x軸于點(diǎn)G,得O、A、C在第一象限的角平分線上,求得A點(diǎn)坐標(biāo),進(jìn)而求得D點(diǎn)坐標(biāo),便可求得結(jié)果.
解:連接OC,AC過A作AE⊥x軸于點(diǎn)E,延長DA與x軸交于點(diǎn)F,過點(diǎn)D作DG⊥x軸于點(diǎn)G,
∵函數(shù)y=![]() (k>12,x>0)的圖象關(guān)于直線AC對稱,
(k>12,x>0)的圖象關(guān)于直線AC對稱,
∴O、A、C三點(diǎn)在同一直線上,且∠COE=45°,
∴OE=AE,
不妨設(shè)OE=AE=a,則A(a,a),
∵點(diǎn)A在在反比例函數(shù)y=![]() (x>0)的圖象上,
(x>0)的圖象上,
∴a2=12,
∴a=![]() ,
,
∴AE=OE=![]() ,
,
∵∠BAD=30°,
∴∠OAF=∠CAD=![]() ∠BAD=15°,
∠BAD=15°,
∵∠OAE=∠AOE=45°,
∴∠EAF=30°,
∴AF=![]() =4,EF=AEtan30°=2,
=4,EF=AEtan30°=2,
∵AB=AD=2,AE∥DG,
∴EF=EG=2,DG=2AE=4![]() ,
,
∴OG=OE+EG=2![]() +2,
+2,
∴D(2![]() +2,4
+2,4![]() ),
),
∴k=![]()
故答案為![]() .
.



| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來源: 題型:
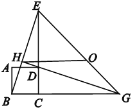
【題目】如圖,四邊形ABCD是正方形,ΔECG是等腰直角三角形,∠BGE的平分線過點(diǎn)D交BE 于H,O是EG的中點(diǎn),對于下面四個結(jié)論:①GH⊥BE;②OH∥BG,且![]() ;③
;③![]() ;④△EBG的外接圓圓心和它的內(nèi)切圓圓心都在直線HG上.其中表述正確的個數(shù)是( )
;④△EBG的外接圓圓心和它的內(nèi)切圓圓心都在直線HG上.其中表述正確的個數(shù)是( )
A.1B.2C.3D.4
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】某市教育行政部門為了解初中學(xué)生參加綜合實(shí)踐活動的情況,隨機(jī)抽取了本市初一、初二、初三年級各![]() 名學(xué)生進(jìn)行了調(diào)查,調(diào)查結(jié)果如圖所示,請你根據(jù)圖中的信息回答問題.
名學(xué)生進(jìn)行了調(diào)查,調(diào)查結(jié)果如圖所示,請你根據(jù)圖中的信息回答問題.
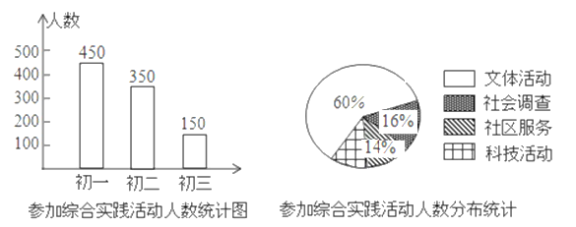
(1)在被調(diào)查的學(xué)生中,參加綜合實(shí)踐活動的有多少人,參加科技活動的有多少人;
(2)如果本市有![]() 萬名初中學(xué)生,請你估計(jì)參加科技活動的學(xué)生約有多少名.
萬名初中學(xué)生,請你估計(jì)參加科技活動的學(xué)生約有多少名.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
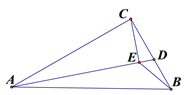
【題目】如圖,在△ABC中,AB=13cm,AC=12cm,BC=5cm.D是BC邊上的一個動點(diǎn),連接AD,過點(diǎn)C作CE⊥AD于E,連接BE,在點(diǎn)D變化的過程中,線段BE的最小值是__cm.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】定義:在平面直角坐標(biāo)系中,將點(diǎn)P繞點(diǎn)T(t,0)(t>0)旋轉(zhuǎn)180°得到點(diǎn)Q,則稱點(diǎn)Q為點(diǎn)P的“發(fā)展點(diǎn)”.
(1)當(dāng)t=3時,點(diǎn)(0,0)的“發(fā)展點(diǎn)”坐標(biāo)為 ,點(diǎn)(﹣1,﹣1)的“發(fā)展點(diǎn)”坐標(biāo)為 .
(2)若t>2,則點(diǎn)(2,3)的“發(fā)展點(diǎn)”的橫坐標(biāo)為 (用含t的代數(shù)式表示 ).
(3)若點(diǎn)P在直線y=2x+6上,其“發(fā)展點(diǎn)”Q在直線y=2x﹣8上,求點(diǎn)T的坐標(biāo).
(4)點(diǎn)P(2,2)在拋物線y=﹣x2+k上,點(diǎn)M在這條拋物線上,點(diǎn)Q為點(diǎn)P的“發(fā)展點(diǎn)”,若△PMQ是以點(diǎn)M為直角頂點(diǎn)的等腰直角三角形,求t的值.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
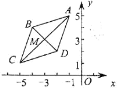
【題目】菱形ABCD在坐標(biāo)平面內(nèi)的位置如圖所示,已知A(-1,5),D(-2,2),對角線交點(diǎn)M(-3,3),如果雙曲線![]() (x<0)與菱形ABCD有公共點(diǎn),那么k的取值范圍是________
(x<0)與菱形ABCD有公共點(diǎn),那么k的取值范圍是________
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
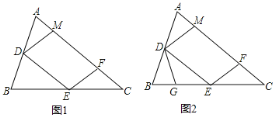
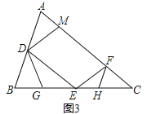
【題目】如圖1,銳角△ABC中,D、E分別是AB、BC的中點(diǎn),F是AC上的點(diǎn),且∠AFE=∠A,DM//EF交AC于點(diǎn)M.
(1)求證:DM=DA;
(2)點(diǎn)G在BE上,且∠BDG=∠C,如圖2,
① 求證:△DEG∽△ECF;
② 從線段CE上取一點(diǎn)H,連接FH使∠CFH=∠B,若BG=1,求EH的長.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,在□ABCD中,E為對角線AC上一點(diǎn),連接DE,作EF⊥DE,交AD于點(diǎn)F,G為AD邊上一點(diǎn),且AB=AG,連接GE.
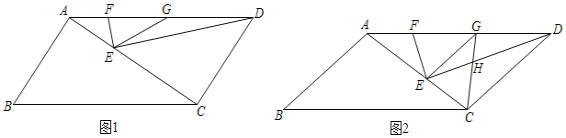
(1)如圖1,若點(diǎn)G為DF的中點(diǎn),AF=2,EG=4,∠B=60°,求AC的長;
(2)如圖2,連接CG交DE于點(diǎn)H,若EG∥CD,∠ACB=∠DCG,求證:∠ECG=2∠AEF.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
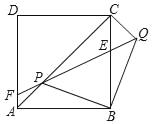
【題目】如圖,正方形ABCD、等腰Rt△BPQ的頂點(diǎn)P在對角線AC上(點(diǎn)P與A、C不重合),QP與BC交于E,QP延長線與AD交于點(diǎn)F,連接CQ.
(1)①求證:AP=CQ;②求證:PA2=AFAD;
(2)若AP:PC=1:3,求tan∠CBQ.
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com