
【題目】如圖,已知∠BAC的平分線與BC的垂直平分線PQ相交于點P,PM⊥AC,PN⊥AB,垂足分別為M、N,AB=5,AC=11,則CM的長度為( )
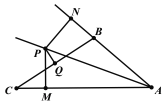
A. 4B. 3C. 2D. 1
【答案】B
【解析】
連接PB,PC,根據角平分線性質求出PM=PN,根據線段垂直平分線求出PB=PC,根據HL證Rt△PMC≌Rt△PNB,Rt△PAN≌Rt△PAM,即可得出答案.
證明:連接PB,PC,
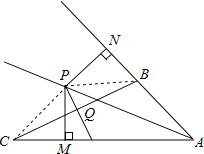
∵AP是∠BAC的平分線,PN⊥AB,PM⊥AC,
∴PM=PN,∠PMC=∠PNB=90°,
∵P在BC的垂直平分線上,
∴PC=PB,
在Rt△PMC和Rt△PNB中
![]() ,
,
∴Rt△PMC≌Rt△PNB(HL),
∴BN=CM.
在Rt△PAN后Rt△PAM中,
![]() ,
,
∴Rt△PAN≌Rt△PAM,
∴AM=AN,
∴AB+AC=AM+CM+AN-BN=2AM=16,
∴AM=8,CM=AC-AM=11-8=3,
故選:B.


 名師指導期末沖刺卷系列答案
名師指導期末沖刺卷系列答案 開心蛙口算題卡系列答案
開心蛙口算題卡系列答案科目:初中數學 來源: 題型:
【題目】如圖1,已知a∥b,點A、B在直線a上,點C、D在直線b上,且AD⊥BC于E.
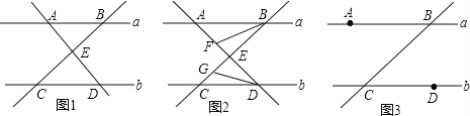
(1)求證:∠ABC+∠ADC=90°;
(2)如圖2,BF平分∠ABC交AD于點F,DG平分∠ADC交BC于點G,求∠AFB+∠CGD的度數;
(3)如圖3,P為線段AB上一點,I為線段BC上一點,連接PI,N為∠IPB的角平分線上一點,且∠NCD=![]() ∠BCN,則∠CIP、∠IPN、∠CNP之間的數量關系是______.
∠BCN,則∠CIP、∠IPN、∠CNP之間的數量關系是______.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】(滿分10分)有一個不透明口袋,裝有分別標有數字1,2,3,4的4個小球(小球除數字不同外,其余都相同),另有3張背面完全一樣、正面分別寫有數字1,2,3的卡片.小敏從口袋中任意摸出一個小球,小穎從這3張背面朝上的卡片中任意摸出一張,然后計算小球和卡片上的兩個數的積.
(1)請你求出摸出的這兩個數的積為6的概率;
(2)小敏和小穎做游戲,她們約定:若這兩個數的積為奇數,小敏贏;否則,小穎贏.你認為該游戲公平嗎?為什么?如果不公平,請你修改游戲規則,使游戲公平.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知:如圖,△ABC的周長為21cm,AB=6cm,BC邊上中線AD=5cm,△ACD周長為16cm,則AC的長為__________cm.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】隨著中國經濟的快速發展以及科技水平的飛速提高,中國高鐵正迅速崛起.高鐵大大縮短了時空距離,改變了人們的出行方式.如圖,![]() ,
,![]() 兩地被大山阻隔,由
兩地被大山阻隔,由![]() 地到
地到![]() 地需要繞行
地需要繞行![]() 地,若打通穿山隧道,建成
地,若打通穿山隧道,建成![]() ,
,![]() 兩地的直達高鐵,可以縮短從
兩地的直達高鐵,可以縮短從![]() 地到
地到![]() 地的路程.已知:
地的路程.已知:![]() ,
,![]() ,
,![]() 公里,求隧道打通后與打通前相比,從
公里,求隧道打通后與打通前相比,從![]() 地到
地到![]() 地的路程將約縮短多少公里?(參考數據:
地的路程將約縮短多少公里?(參考數據:![]() ,
,![]() )
)

查看答案和解析>>
科目:初中數學 來源: 題型:
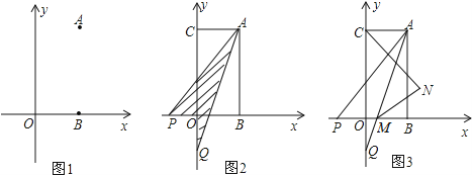
【題目】如圖:已知在平面直角坐標系中點A(a,b)點B(a,0),且滿足|2a-b|+(b-4)2=0.
(1)求點A、點B的坐標;
(2)已知點C(0,b),點P從B點出發沿x軸負方向以1個單位每秒的速度移動.同時點Q從C點出發,沿y軸負方向以2個單位每秒的速度移動,某一時刻,如圖所示且S陰=![]() S四邊形OCAB,求點P移動的時間;
S四邊形OCAB,求點P移動的時間;
(3)在(2)的條件下,AQ交x軸于M,作∠ACO,∠AMB的角平分線交于點N,判斷![]() 是否
是否![]() 為定值,若是定值求其值;若不是定值,說明理由.
為定值,若是定值求其值;若不是定值,說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】七年級進行法律知識競賽,共有30道題,答對一道題得4分,不答或答錯一道題扣2分.
(1)小紅同學參加了競賽,成績是90分,請問小紅在競賽中答對了多少道題?
(2)小明也參加了競賽,考完后他說:“這次競賽我一定能拿到100分.”請問小明有沒有可能拿到100分?試用方程的知識來說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】定義一次函數y=px+q的特征數為[p,q].如:y=3x-1的特征數是[3,-1]
(1)若某正比例函數的特征數是[k+2, ![]() ],求k的值.
],求k的值.
(2)在平面直角坐標系中,有兩點A(-m,0),B(0,-2m),且△OAB的面積為4(O為原點),求過A、B兩點的一次函數的特征數.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com