
【題目】如圖,AB是⊙O的直徑,BC是⊙O的切線,D是⊙O上的一點,且AD∥CO,連結CD 
(1)求證:CD是⊙O的切線;
(2)若AB=2,CD= ![]() ,求AD的長.(結果保留根號)
,求AD的長.(結果保留根號)
【答案】
(1)證明:連接OD,
∵AD∥OC,
∴∠1=∠3,∠2=∠4
∵OA=OD
∴∠3=∠4
∴∠1=∠2,
在△OCB與△OCD中. 
∴△OCB≌△OCD.(SAS).
∴∠ODC=∠OBC.
∵BC是⊙O的切線
∴∠OBC=90°.
∴∠ODC=90°.
∴OD⊥CD.
∴CD切⊙O于D;
(2)解:由(1)知:CD、BC是⊙O的切線,
∴BC=CD= ![]() ,
,
在Rt△OCB中,
∵OB= ![]() AB=1,
AB=1,
∴OC= ![]() ,
,
由(1)知:∠2=∠4,
∵AB是直徑,
∴∠ADB=90°.
∴∠ADB=∠ABC=90°.
∴△OCB∽△ABD,
∴ ![]()
即 ![]() ,
,
∴ ![]() ;
;

【解析】(1)連接OD,SAS證明△ODC≌△OBC,得出∠CDO=∠CBO=90°,即可得出CD是⊙O的切線;(2)先求出OB,OC的長,再運用△ADB∽△OBC,求出AD的長.
【考點精析】解答此題的關鍵在于理解相似三角形的判定與性質的相關知識,掌握相似三角形的一切對應線段(對應高、對應中線、對應角平分線、外接圓半徑、內切圓半徑等)的比等于相似比;相似三角形周長的比等于相似比;相似三角形面積的比等于相似比的平方.


 輕松課堂單元期中期末專題沖刺100分系列答案
輕松課堂單元期中期末專題沖刺100分系列答案科目:初中數學 來源: 題型:
【題目】列方程或方程組解應用題:
為了響應“十三五”規劃中提出的綠色環保的倡議,某校文印室提出了每個人都踐行“雙面打印,節約用紙”.已知打印一份資料,如果用A4厚型紙單面打印,總質量為400克,將其全部改成雙面打印,用紙將減少一半;如果用A4薄型紙雙面打印,這份資料的總質量為160克,已知每頁薄型紙比厚型紙輕0.8克,求A4薄型紙每頁的質量.(墨的質量忽略不計)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在ABCD中,E是BC的中點,連接AE并延長交DC的延長線于點F. 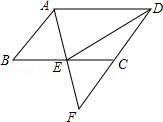
(1)求證:AB=CF;
(2)連接DE,若AD=2AB,求證:DE⊥AF.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知AB∥CD,分別探究下面兩個圖形中∠APC和∠PAB、∠PCD的關系,請從你所得兩個關系中選出任意一個,說明你探究的結論的正確性.

結論:(1)
(2)
選擇結論: ,說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】一項工程,甲,乙兩公司合作,12天可以完成;如果甲,乙兩公司單獨完成此項工程,乙公司所用時間是甲公司的1.5倍,乙公司每天的施工費比甲公司每天的施工費少1500元.
(1)甲,乙兩公司單獨完成此項工程,各需多少天?
(2)若讓一個公司單獨完成這項工程,要使乙公司的總施工費較少,則甲公司每天的施工費應低于多少元?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,直線AB:y=kx+2k交x軸于點A,交y軸正半軸于點B,且S△OAB=3
(1) 求A、B兩點的坐標
(2) 將直線AB繞A點順時針旋轉45°,交y軸于點C,求直線AC的解析式.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖:邊長為12的大正方形中有兩個小正方形,若兩個小正方形的面積分別為S1、S2 , 則S1+S2的值為( ) 
A.60
B.64
C.68
D.72
查看答案和解析>>
科目:初中數學 來源: 題型:
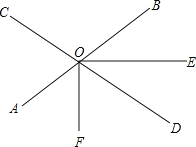
【題目】如圖,直線AB、CD相交于O點,∠AOC=70,OF平分∠AOD,射線OE在∠BOD的內部(如圖),∠BOE=n°.
(1)當n=30時,求∠DOE的度數;
(2)當n=35時,射線OE與OF之間有什么位置關系?
(3)若射線OD平分∠EOF,求n的值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com