
【題目】如圖,在平面直角坐標系中,點![]() 在
在![]() 軸正半軸上,
軸正半軸上,![]() 軸,點
軸,點![]() 的橫坐標都是
的橫坐標都是![]() ,且
,且![]() ,點
,點![]() 在
在![]() 上,若反比例函數
上,若反比例函數![]() 的圖象經過點
的圖象經過點![]() ,且
,且![]() .
.
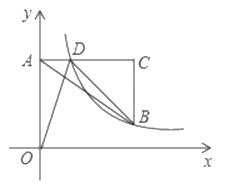
(1)求點![]() 坐標;
坐標;
(2)將![]() 沿著
沿著![]() 折疊,設頂點
折疊,設頂點![]() 的對稱點為
的對稱點為![]() ,試判斷點
,試判斷點![]() 是否恰好落在直線
是否恰好落在直線![]() 上,為什么.
上,為什么.
【答案】(1)![]() ;(2)
;(2)![]() 不在直線
不在直線![]() 上,理由見解析
上,理由見解析
【解析】
(1)先根據AO:BC=3:2,BC=2得出OA的長,再根據點B、C的橫坐標都是3可知BC∥AO,故可得出B點坐標,再根據點B在反比例函數y=![]() (x>0)的圖象上可求出k的值,由AC∥x軸可設點D(t,3)代入反比例函數的解析式即可得出t的值,進而得出D點坐標;
(x>0)的圖象上可求出k的值,由AC∥x軸可設點D(t,3)代入反比例函數的解析式即可得出t的值,進而得出D點坐標;
(2)過點A′作EF∥OA交AC于E,交x軸于F,連接OA′,根據AC∥x軸可知∠A′ED=∠A′FO=90°,由相似三角形的判定定理得出△DEA′∽△A′FO,設A′(m,n),可得出![]() ,再根據勾股定理可得出m2+n2=9,兩式聯立可得出m、n的值,故可得出A′的坐標,用待定系數法求出經過點D(1,3),點B(3,1)的直線函數關系式為y=-x+4,再把x=
,再根據勾股定理可得出m2+n2=9,兩式聯立可得出m、n的值,故可得出A′的坐標,用待定系數法求出經過點D(1,3),點B(3,1)的直線函數關系式為y=-x+4,再把x=![]() 代入即可得出結論.
代入即可得出結論.
(1)解:(1)∵AO:BC=3:2,BC=2,
∴OA=3,
∵點B、C的橫坐標都是3,
∴BC∥AO,
∴B(3,1),
∵點B在反比例函數y=![]() (x>0)的圖象上,
(x>0)的圖象上,
∴1=![]() ,解得k=3,
,解得k=3,
∵AC∥x軸,
∴設點D(t,3),
∴3t=3,解得t=1,
∴D(1,3);
(2)結論:點A′不在此反比例函數的圖象上.
理由:過點A′作EF∥OA交AC于E,交x軸于F,連接OA′(如圖所示),

∵AC∥x軸,
∴∠A′ED=∠A′FO=90°,
∵∠OA′D=90°,
∴∠A′DE=∠OA′F,
∴△DEA′∽△A′FO,
設A′(m,n),
∴![]() ,
,
又∵在Rt△A′FO中,m2+n2=9,
∴m=![]() ,n=
,n=![]() ,即A′(
,即A′(![]() ,
,![]() ),
),
設直線BD的解析式為y=kx+b,
∵點D(1,3),點B(3,1)在y=kx+b,
![]() ,
,
∴![]() ,
,
∴y=-x+4,
∴當x=![]() 時,y=
時,y= ![]() ,
,
∴點A′不在直線BD上.


科目:初中數學 來源: 題型:
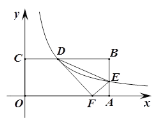
【題目】如圖,矩形OABC的邊OA、OC分別在x軸、y軸上,點B 的坐標為(8,4),反比例函數y=![]() (k>0)的圖象分別交邊BC、AB 于點D、E,連結DE,△DEF與△DEB關于直線DE對稱,當點F恰好落在線段OA上時,則k的值是________.
(k>0)的圖象分別交邊BC、AB 于點D、E,連結DE,△DEF與△DEB關于直線DE對稱,當點F恰好落在線段OA上時,則k的值是________.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】蕪湖市某醫院計劃選購A,B兩種防護服.已知A防護服每件價格是B防護服每件價格的2倍,用80000元單獨購買A防護服比用80000元單獨購買B防護服要少50件.如果該醫院計劃購買B防護服的件數比購買A防護服件數的2倍多8件,且用于購買A,B兩種防護服的總經費不超過320000元,那么該醫院最多可以購買多少件B防護服?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,拋物線y=﹣2x2+8x﹣6與x軸交于點A、B,把拋物線在x軸及其上方的部分記作C1,將C1向右平移得C2,C2與x軸交于點B,D.若直線y=x+m與C1、C2共有3個不同的交點,則m的取值范圍是( )

A. ﹣2<m<![]() B. ﹣3<m<﹣
B. ﹣3<m<﹣![]() C. ﹣3<m<﹣2 D. ﹣3<m<﹣
C. ﹣3<m<﹣2 D. ﹣3<m<﹣![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知:如圖①,在矩形ABCD中,AB=5,![]() ,AE⊥BD,垂足是E.點F是點E關于AB的對稱點,連接AF、BF.
,AE⊥BD,垂足是E.點F是點E關于AB的對稱點,連接AF、BF.
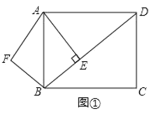
(1)求AE和BE的長;
(2)若將△ABF沿著射線BD方向平移,設平移的距離為m(平移距離指點B沿BD方向所經過的線段長度).當點F分別平移到線段AB、AD上時,求出相應的m的值;
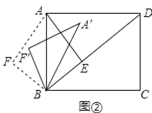
(3)如圖②,將△ABF繞點B順時針旋轉一個角α(0°<α<180°),記旋轉中的![]() 為
為![]() ,在旋轉過程中,設
,在旋轉過程中,設![]() 所在的直線與直線AD交于點P,與直線BD交于點Q,若△DPQ為等腰三角形,請直接寫出此時DQ的長.
所在的直線與直線AD交于點P,與直線BD交于點Q,若△DPQ為等腰三角形,請直接寫出此時DQ的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】2020賀歲片《囧媽》提檔大年三十網絡首播.“樂調查”平臺為了全面了解觀眾對《囧媽》的滿意度情況,進行隨機抽樣調查,分為四個類別:![]() .非常滿意;
.非常滿意;![]() .滿意;
.滿意;![]() .基本滿意;
.基本滿意;![]() .不滿意,依據調查數據繪制成圖1和圖2的統計圖(不完整).
.不滿意,依據調查數據繪制成圖1和圖2的統計圖(不完整).
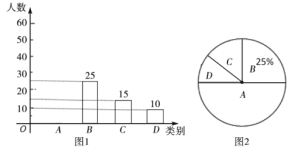
根據以上信息,解答下列問題:
(1)本次接受調查的觀眾共有_______人;
(2)扇形統計圖中,扇形![]() 的圓心角度數是_______;
的圓心角度數是_______;
(3)請補全條形統計圖;
(4)“樂調查”平臺調查了春節期間觀看《固媽》的觀眾約5000人,請估計觀眾對該電影的滿意(![]() 、
、![]() 、
、![]() 類視為滿意)的人數.
類視為滿意)的人數.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖1,AB是半圓O的直徑,正方形OPNM的對角線ON與AB垂直且相等,Q是OP的中點.一只機器甲蟲從點A出發勻速爬行,它先沿直徑爬到點B,再沿半圓爬回到點A,一臺微型記錄儀記錄了甲蟲的爬行過程.設甲蟲爬行的時間為t,甲蟲與微型記錄儀之間的距離為y,表示y與t的函數關系的圖象如圖2所示,那么微型記錄儀可能位于圖1中的( )
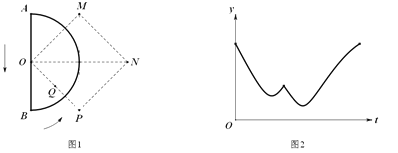
A.點MB.點NC.點PD.點Q
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】閱讀理解:給定一個矩形,如果存在另一個矩形,它的周長和面積分別是已知矩形的周長和面積的一半,則這個矩形是給定矩形的“減半”矩形.如圖,矩形![]() 是矩形
是矩形![]() 的“減半”矩形.
的“減半”矩形.
請你解決下列問題:
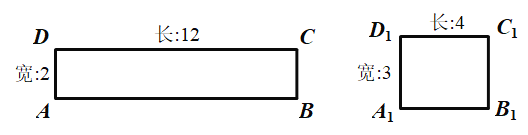
(1)當矩形的長和寬分別為![]() ,
,![]() 時,它是否存在“減半”矩形?請作出判斷,并說明理由.
時,它是否存在“減半”矩形?請作出判斷,并說明理由.
(2)邊長為![]() 的正方形存在“減半”正方形嗎?如果存在,求出“減半”正方形的邊長;如果不存在,請說明理由.
的正方形存在“減半”正方形嗎?如果存在,求出“減半”正方形的邊長;如果不存在,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在一個不透明的盒子中裝有4張卡片.4張卡片的正面分別標有數字1,2,3,4,這些卡片除數字外都相同,將卡片攪勻.
(1)從盒子任意抽取一張卡片,恰好抽到標有奇數卡片的概率是: ;
(2)先從盒子中任意抽取一張卡片,再從余下的3張卡片中任意抽取一張卡片,求抽取的2張卡片標有數字之和大于4的概率(請用畫樹狀圖或列表等方法求解).
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com