
【題目】(10分)將一副三角尺如圖拼接:含30°角的三角尺(△ABC)的長直角邊與含45°角的三角尺(△ACD)的斜邊恰好重合.已知AB=2![]() ,P是AC上的一個動點.
,P是AC上的一個動點.

(1)當點P運動到∠ABC的平分線上時,連接DP,求DP的長;
(2)當點P在運動過程中出現PD=BC時,求此時∠PDA的度數;
(3)當點P運動到什么位置時,以D,P,B,Q為頂點的平行四邊形的頂點Q恰好在邊BC上?求出此時□DPBQ的面積.
【答案】(1)DP的長為![]()
(2)∠PDA的度數為75°;
(3)點CP長為![]() 時,此時□DPBQ的面積為
時,此時□DPBQ的面積為![]()
【解析】解:在Rt△ABC中,AB=2![]() ,∠BAC=30°,∴BC=
,∠BAC=30°,∴BC=![]() ,AC=3.
,AC=3.
(1)如圖(1),作DF⊥AC,∵Rt△ACD中,AD=CD,∴DF=AF=CF=![]() .
.
∵BP平分∠ABC,∴∠PBC=30°,∴CP=BC·tan30°=1,∴PF=![]() ,∴DP=
,∴DP=![]() =
=![]() .
.
(2)當P點位置如圖(2)所示時,根據(1)中結論,DF=![]() ,∠ADF=45°,又PD=BC=
,∠ADF=45°,又PD=BC=![]() ,∴cos∠PDF=
,∴cos∠PDF=![]() =
=![]() ,∴∠PDF=30°.
,∴∠PDF=30°.
∴∠PDA=∠ADF-∠PDF=15°.
當P點位置如圖(3)所示時,同(2)可得∠PDF=30°.
∴∠PDA=∠ADF+∠PDF=75°.
(3)CP=![]() .
.
在□DPBQ中,BC∥DP,∵∠ACB=90°,∴DP⊥AC.根據(1)中結論可知,DP=CP=![]() ,∴S□DPBQ=
,∴S□DPBQ=![]() =
=![]() .
.


 名校課堂系列答案
名校課堂系列答案科目:初中數學 來源: 題型:
【題目】某商場為了吸引顧客,設計了一種促銷活動:在一個不透明的箱子里放有4個相同的小球,球上分別標有“0元”、“10元”、“20元”和“30元”的字樣.規定:顧客在本商場同一日內,每消費滿200元,就可以在箱子里先后摸出兩個球(第一次摸出后不放回),商場根據兩小球所標金額的和返還相應價格購物券,可以重新在本商場消費,某顧客剛好消費200元.
(1)該顧客至少可得到_____元購物券,至多可得到_______元購物券;
(2)請你用畫樹狀圖或列表的方法,求出該顧客所獲得購物券的金額不低于30元的概率.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在平面直角坐標系中,B點坐標為(x、y),且x、y滿足|x+y﹣8|+(x﹣y)2=0.
(1)求B點坐標;
(2)如圖,點A為y軸正半軸上一點,過點B作BC⊥AB,交x軸正半軸于點C,求證:AB=BC. 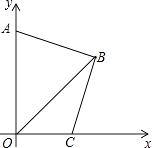
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某學校初一年級參加社會實踐課,報名第一門課的有x人,第二門課的人數比第一門課的 ![]() 少20人,現在需要從報名第二門課的人中調出10人學習第一門課,那么:
少20人,現在需要從報名第二門課的人中調出10人學習第一門課,那么:
(1)報兩門課的共有多少人?
(2)調動后,報名第一門課的人數為人,第二門課人數為人.
(3)調動后,報名第一門課比報名第二門課多多少人?計算出代數式后,請選擇一個你覺得合適的x的值代入,并求出具體的人數.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,△ABC中∠A=30°,E是AC邊上的點,先將△ABE沿著BE翻折,翻折后△ABE的AB邊交AC于點D,又將△BCD沿著BD翻折,C點恰好落在BE上,此時∠CDB=82°,則原三角形的∠B為( ) 
A.75°
B.76°
C.77°
D.78°
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,一次函數y=kx+b(k<0)與反比例函數![]() 的圖象相交于A、B兩點,一次函數的圖象與y軸相交于點C,已知點A(4,1)
的圖象相交于A、B兩點,一次函數的圖象與y軸相交于點C,已知點A(4,1)

(1)求反比例函數的解析式;
(2)連接OB(O是坐標原點),若△BOC的面積為3,求該一次函數的解析式.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com