【題目】如圖，
，
，點
在
軸上，且
．
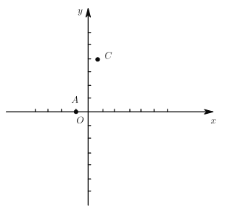
（1）求點的坐標；
（2）求
的面積；
（3）在
軸上是否存在點
，使以
、、三點為頂點的三角形的面積為10？若存在，請直接寫出點的坐標．若不存在，請說明理由．
【答案】（1）（2,0）或（-4,0）;（2）=6;（3）（0，
）或（0，-）．
【解析】
(1)分點B在點A的左邊和右邊兩種情況解答;
(2)利用三角形的面積公式列式計算即可得解;
（3）利用三角形的面積公式列式求出點P到x軸的距離,然后分兩種情況寫出點P的坐標即可.
解:（1）點B在點A的右邊時,-1+3=2, 點B在點A的左邊時,-1-3=-4,
所以,B的坐標為（2,0）或（-4,0）;
（2）△ABC的面積=
×3×4=6;
（3）設點P到x軸的距離為h,
則×3h=10, 解得h=,
點P在y軸正半軸時,P（0，）, 點P在y軸負半軸時,P（0，-），
綜上所述,點P的坐標為（0，）或（0，-）．
科目：初中數學 來源： 題型：
【題目】如圖，在Rt△ABC中，∠ACB=90°，AO是△ABC的角平分線．以O為圓心，OC為半徑作⊙O．
（1）求證：AB是⊙O的切線．
（2）已知AO交⊙O于點E，延長AO交⊙O于點D，tanD=
，求
的值．
（3）在（2）的條件下，設⊙O的半徑為3，求AB的長．
【答案】（1）證明見解析（2）
（3）
【解析】試題分析：（1）過O作OF⊥AB于F，由角平分線上的點到角兩邊的距離相等即可得證；（2）連接CE，證明△ACE∽△ADC可得
= tanD＝
；（3）先由勾股定理求得AE的長，再證明△B0F∽△BAC，得
，設BO="y" ，BF=z，列二元一次方程組即可解決問題．
試題解析：（1）證明：作OF⊥AB于F
∵AO是∠BAC的角平分線，∠ACB=90
∴OC=OF
∴AB是⊙O的切線
（2）連接CE
∵AO是∠BAC的角平分線，
∴∠CAE=∠CAD
∵∠ACE所對的弧與∠CDE所對的弧是同弧
∴∠ACE=∠CDE
∴△ACE∽△ADC
∴= tanD＝
（3）先在△ACO中，設AE=x,
由勾股定理得
(x＋3)="(2x)" ＋3 ，解得x="2,"
∵∠BFO=90°=∠ACO
易證Rt△B0F∽Rt△BAC
得，
設BO=y BF=z
即4z=9＋3y，4y=12＋3z
解得z=
y=
∴AB=＋4=
考點：圓的綜合題．
【題型】解答題
【結束】
22
【題目】已知：二次函數
的圖象與x軸交于A、B兩點，與y軸交于點C，其中點B在x軸的正半軸上，點C在y軸的正半軸上，線段OB、OC的長（OB＜OC）是方程x2－10x＋16＝0的兩個根，且A點坐標為（－6，0）．
（1）求此二次函數的表達式；
（2）若點E是線段AB上的一個動點（與點A、點B不重合），過點E作EF∥AC交BC于點F，連接CE，設AE的長為m，△CEF的面積為S，求S與m之間的函數關系式，并寫出自變量m的取值范圍；
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】已知，如圖直線
的解析式為
，直線
的解析式為
；這兩個圖象交于
軸上一點
，直線與
軸的交點
動點
從點
出發沿軸以每秒1個單位長的速度向左移動，設移動時間為
秒，當
__________時，
為等腰三角形．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，BC是路邊坡角為30°，長為10米的一道斜坡，在坡頂燈桿CD的頂端D處有一探射燈，射出的邊緣光線DA和DB與水平路面AB所成的夾角∠DAN和∠DBN分別是37°和60°（圖中的點A、B、C、D、M、N均在同一平面內，CM∥AN）．
（1）求燈桿CD的高度；
（2）求AB的長度（結果精確到0.1米）．（參考數據：
=1.73．sin37°≈060，cos37°≈0.80，tan37°≈0.75）
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】已知：
是
的角平分線，點
，
分別在
，
上，且
，
（1）如圖1，求證：四邊形
是平行四邊形；
（2）如圖2，若為等邊三角形，在不添加輔助線的情況下，請你直接寫出所有的全等三角形.
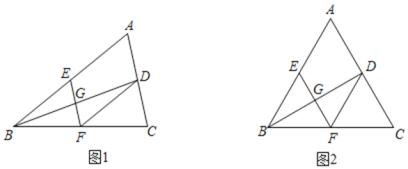
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】若x＝﹣m和x＝m﹣4時，多項式ax2+bx+4a+1的值相等，且m≠2．當﹣1＜x＜2時，存在x的值，使多項式ax2+bx+4a+1的值為3，則a的取值范圍是______．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，在Rt△ABC中，AB=AC=4
．一動點P從點B出發，沿BC方向以每秒1個單位長度的速度勻速運動，到達點C即停止．在整個運動過程中，過點P作PD⊥BC與Rt△ABC的直角邊相交于點D，延長PD至點Q，使得PD=QD，以PQ為斜邊在PQ左側作等腰直角三角形PQE．設運動時間為t秒（t＞0）．
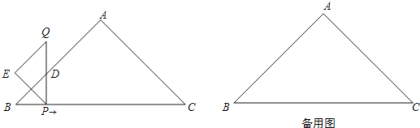
(1)在整個運動過程中，設△ABC與△PQE重疊部分的面積為S，請直接寫出S與t之間的函數關系式以及相應的自變量t的取值范圍；
(2)當點D在線段AB上時，連接AQ、AP，是否存在這樣的t，使得△APQ成為等腰三角形？若存在，求出對應的t的值；若不存在，請說明理由；
(3)當t=4秒時，以PQ為斜邊在PQ右側作等腰直角三角形PQF，將四邊形PEQF繞點P旋轉，PE與線段AB相交于點M，PF與線段AC相交于點N．試判斷在這一旋轉過程中，四邊形PMAN的面積是否發生變化？若發生變化，求出四邊形PMAN的面積y與PM的長x之間的函數關系式以及相應的自變量x的取值范圍；若不發生變化，求出此定值．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com