
【題目】某公司為了擴大經營,決定購進6臺機器用于生產某種活塞.現有甲、乙兩種機器供選擇,其中每種機器的價格和每臺機器日生產活塞的數量如下表所示,經過預算,本次購買機器所耗資金不能超過34萬元.
甲 | 乙 | |
價格(萬元/臺) | 7 | 5 |
每臺日產量(個) | 100 | 60 |
(1)按該公司要求可以有幾種購買方案?
(2)若該公司購進的6臺機器的日生產能力不能低于380個,那么為了節約資金應選擇哪種購買方案?
【答案】(1)見解析;(2)應選擇方案一
【解析】分析:(1)設購買甲種機器x臺(x≥0),則購買乙種機器(6-x)臺,根據買機器所耗資金不能超過34萬元,即購買甲種機器的錢數+購買乙種機器的錢數≤34萬元.就可以得到關于x的不等式,就可以求出x的范圍.
(2)該公司購進的6臺機器的日生產能力不能低于380個,就是已知不等關系:甲種機器生產的零件數+乙種機器生產的零件數≤380件.根據(1)中的三種方案,可以計算出每種方案的需要資金,從而選擇出合適的方案.
詳解:
(1)設購買甲種機器x臺(x≥0),則購買乙種機器(6-x)臺
依題意,得7x+5×(6-x)≤34
解這個不等式,得x≤2,即x可取0,1,2三個值.
∴該公司按要求可以有以下三種購買方案:
方案一:不購買甲種機器,購買乙種機器6臺.
方案二:購買甲種機器l1臺,購買乙種機器5臺.
方案三:購買甲種機器2臺,購買乙種機器4臺
(2)根據題意,100x+60(6-x)≥380
解之得x>![]()
由(1)得x≤2,即![]() ≤x≤2.
≤x≤2.
∴x可取1,2倆值.
即有以下兩種購買方案:
方案一購買甲種機器1臺,購買乙種機器5臺,所耗資金為1×7+5×5=32萬元;方案二購買甲種機器2臺,購買乙種機器4臺,所耗資金為2×7+4×5=34萬元.
∴為了節約資金應選擇方案一.
故應選擇方案一


科目:初中數學 來源: 題型:
【題目】如圖,動點P在平面直角坐標系中按圖中箭頭所示方向運動,第1次從原點運動到點(1,1),第2次接著運動到點(2,0),第3次接著運動到點(3,2),…,按這樣的運動規律,經過第2016次運動后,動點P的坐標是( )
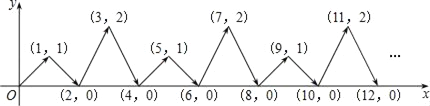
A. (2016,1) B. (2016,0) C. (2016,2) D. (2017,0)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖所示,在△ABC中,DM,EN分別垂直平分AB和AC,交BC于點D,E,若∠DAE=50°°,則∠BAC=________,若△ADE的周長為19cm,則BC=_____cm.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,四邊形ABCD是正方形,其中A(1,1),B(3,1),D(1,3).反比例函數 ![]() 的圖象經過對角線BD的中點M,與BC,CD的邊分別交于點P、Q.
的圖象經過對角線BD的中點M,與BC,CD的邊分別交于點P、Q.
(1)直接寫出點M,C的坐標;
(2)求直線BD的解析式;
(3)線段PQ與BD是否平行?并說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,剪兩張對邊平行且寬度相等的紙條隨意交叉疊放在一起,轉動其中一張,重合部分構成一個四邊形,則下列結論中不一定成立的是( )

A. ∠ABC=∠ADC,∠BAD=∠BCD B. AB=BC
C. AB=CD,AD=BC D. ∠DAB+∠BCD=180°
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖①,![]() 平分
平分![]() ,
,![]() ⊥
⊥![]() ,
,![]() ,
,![]() .
.
【1】求![]() 的度數
的度數
【2】如圖②,若把“![]() ⊥
⊥![]() ”變成“點F在DA的延長線上,
”變成“點F在DA的延長線上,![]() ”,其它條件不變,求
”,其它條件不變,求![]() 的度數;
的度數;
【3】如圖③,若把“![]() ⊥
⊥![]() ”變成“
”變成“![]() 平分
平分![]() ”,其它條件不變,
”,其它條件不變,![]() 的大小是否變化,并請說明理由.(此題9分)
的大小是否變化,并請說明理由.(此題9分)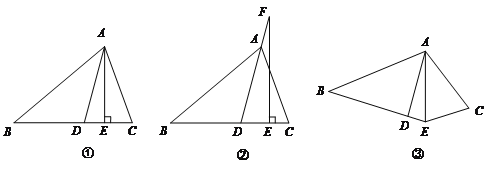
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】有若干個數,第一個數記為a1,第二個數記為a2,第三個數記為a3,…,第n個數記為an,若a1=![]() ,從第二個數起,每個數都等于“1與它前面那個數差的倒數”.
,從第二個數起,每個數都等于“1與它前面那個數差的倒數”.
(1)計算:a2 ,a3 ,a4 ,a5的值;
(2)這排數有什么規律?由你發現的規律,計算a2014的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】有![]() 箱桔子,以每箱
箱桔子,以每箱![]() 千克為標準,稱重記錄如下(單位:千克,超過標準的千克數為正數,不足標準的千克數記為負數):
千克為標準,稱重記錄如下(單位:千克,超過標準的千克數為正數,不足標準的千克數記為負數):![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
![]() 稱得的
稱得的![]() 箱總質量與標準總質量相比超過或不足多少千克?
箱總質量與標準總質量相比超過或不足多少千克?
![]() 若每箱桔子進價
若每箱桔子進價![]() 元/千克,售價
元/千克,售價![]() 元/千克,則這
元/千克,則這![]() 箱桔子全部售出共盈利多少錢?
箱桔子全部售出共盈利多少錢?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com