
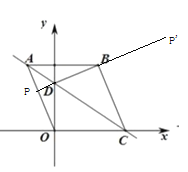
【題目】如圖,四邊形![]() 是菱形,以點
是菱形,以點![]() 為坐標原點,
為坐標原點,![]() 所在直線為
所在直線為![]() 軸建立平面直角坐標系.若點
軸建立平面直角坐標系.若點![]() 的坐標為
的坐標為![]() ,直線
,直線![]() 與
與![]() 軸相交于點
軸相交于點![]() ,連接
,連接![]() .
.
(1)求菱形![]() 的邊長;
的邊長;
(2)證明![]() 為直角三角形;
為直角三角形;
(3)直線![]() 上是否存在一點
上是否存在一點![]() 使得
使得![]() 的面積與
的面積與![]() 的面積相等?若存在,請求出點
的面積相等?若存在,請求出點![]() 的坐標;若不存在,請說明理由.
的坐標;若不存在,請說明理由.


【答案】(1)13;(2)證明見解析;(3)![]() 為
為![]() 或
或![]() .
.
【解析】
(1)過點![]() 作
作![]() 軸于點
軸于點![]() ,利用A點坐標及勾股定理即可求解;
,利用A點坐標及勾股定理即可求解;
(2)根據(jù)菱形的性質(zhì)求出B,C點坐標,再求出AC的解析式,進而求出D點坐標,利用待定系數(shù)法求出直線BD,BC的解析式,根據(jù)k的值即可判斷;
(3)根據(jù)△![]() 與
與![]() 的面積相等,故同底等高,于是延長BD交AO于P,即為所求,聯(lián)立兩直線的解析式即可求出P點坐標,再根據(jù)對稱性求出另一點坐標.
的面積相等,故同底等高,于是延長BD交AO于P,即為所求,聯(lián)立兩直線的解析式即可求出P點坐標,再根據(jù)對稱性求出另一點坐標.
解(1)過點![]() 作
作![]() 軸于點
軸于點![]() ,
,
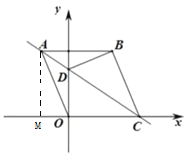
![]() ,
,![]() ,
,
∴![]()
(2)∵![]() 為菱形,∴
為菱形,∴![]() ,
,
∴![]()
又∵![]() ,
,
∴![]()
又∵![]() ,
,
設(shè)直線AC的解析式為y=kx+b(k≠0)
把A,C代入得![]() ,
,
解得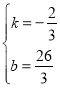 ,
,
∴![]() ,
,
令x=0,y=![]() ,
,
∴點![]()
設(shè)直線BC的解析式為y=px+q(p≠0)
把B,C代入得![]() ,
,
解得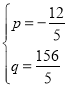 ,
,
∴![]() ,
,
設(shè)直線BD的解析式為y=mx+n(m≠0)
把B,D代入得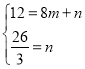 ,
,
解得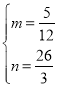 ,
,
∴![]() ,
,
∴![]()
∵![]() ,
,
∴![]()
所以![]() 為直角三角形;
為直角三角形;
(3)延長![]() 交
交![]() 于點
于點![]() ,
,
∵![]() ,
,
∴![]()
∵![]() ,
,
設(shè)直線AO的解析式為y=cx(c≠0),
把A代入得12=-5c,
解得c=![]() ,
,
∴![]() ,
,
由(2)知![]() 聯(lián)立得:
聯(lián)立得:
![]() ,
,
解得![]() ,
,
所以點![]() ,
,
作![]() 關(guān)于點
關(guān)于點![]() 的對稱點
的對稱點![]() ,
,
設(shè)P’(x,y),
可根據(jù)中點得: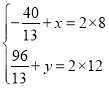 ,
,
解得 ,
,
∴![]() ,
,
綜上點![]() 為
為![]() 或
或![]() .
.


科目:初中數(shù)學 來源: 題型:
【題目】如圖,矩形ABCD中,BC=7cm,CD=5cm,P、Q兩點分別從B、C兩點同時出發(fā),沿矩形ABCD的邊以1cm/s的速度逆時針運動,點P到達點C時兩點同時停止運動.當點P的運動時間為_s時,△PQC為等腰三角形.

查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】(本題滿分![]() 分)小明、小華在一棟高樓前感慨樓房真高.小明說:“這樓起碼
分)小明、小華在一棟高樓前感慨樓房真高.小明說:“這樓起碼![]() 層!”小華卻不以為然:“
層!”小華卻不以為然:“![]() 層?我看沒有!”小明說:“有本事,就讓我們一起來測量吧!”
層?我看沒有!”小明說:“有本事,就讓我們一起來測量吧!”
如圖,矩形![]() 表示樓體,小明、小華在樓體兩側(cè)各選
表示樓體,小明、小華在樓體兩側(cè)各選![]() 、
、![]() 兩點,使得
兩點,使得![]() 、
、![]() 、
、![]() 、
、![]() 四點在同一直線上,利用皮尺和側(cè)傾器測得如下數(shù)據(jù),
四點在同一直線上,利用皮尺和側(cè)傾器測得如下數(shù)據(jù), ![]() 米,
米, ![]() 米,
米, ![]() ,
, ![]() .
.
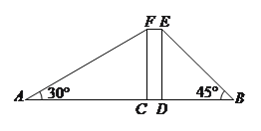
(![]() )請你幫助他們算一算樓高.(結(jié)果保留根號)
)請你幫助他們算一算樓高.(結(jié)果保留根號)
(![]() )若每層樓按
)若每層樓按![]() 米計算,你支持小明還是小華的觀點呢?請說明理由.
米計算,你支持小明還是小華的觀點呢?請說明理由.
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】四邊形ABCD中,對角線AC、BD相交于點O,下列條件不能判定這個四邊形是平行四邊形的是

A.AB∥DC,AD∥BC B.AB=DC,AD=BC
C.AO=CO,BO=DO D.AB∥DC,AD=BC
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】如圖,![]() ,
,![]() 平分
平分![]() .將一塊足夠大的三角尺的直角頂點落在射線
.將一塊足夠大的三角尺的直角頂點落在射線![]() 的任意一點
的任意一點![]() 上,并使三角尺的一條直角邊與
上,并使三角尺的一條直角邊與![]() (或
(或![]() 的延長線)交于點
的延長線)交于點![]() ,另一條直角邊與
,另一條直角邊與![]() 交于點
交于點![]() .
.

(1)如圖1,當![]() 與邊
與邊![]() 垂直時,證明:
垂直時,證明:![]() ;
;
(2)如圖2,把三角尺繞點![]() 旋轉(zhuǎn),三角尺的兩條直角邊分別交
旋轉(zhuǎn),三角尺的兩條直角邊分別交![]() 于點
于點![]() ,在旋轉(zhuǎn)過程中,
,在旋轉(zhuǎn)過程中,![]() 與
與![]() 相等嗎?請直接寫出結(jié)論:
相等嗎?請直接寫出結(jié)論:![]()
![]() (填
(填![]() ,
,![]() ,
,![]() ),
),
(3)如圖3,三角尺繞點![]() 繼續(xù)旋轉(zhuǎn),三角尺的一條直角邊與
繼續(xù)旋轉(zhuǎn),三角尺的一條直角邊與![]() 的延長線交于點
的延長線交于點![]() ,另一條直角邊與
,另一條直角邊與![]() 交于點
交于點![]() .在旋轉(zhuǎn)過程中,
.在旋轉(zhuǎn)過程中,![]() 與
與![]() 相等嗎?若相等,請給出證明;若不相等,請說明理由.
相等嗎?若相等,請給出證明;若不相等,請說明理由.
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】如圖,Rt△ABC中,AB=AC=8,BO=![]() AB,點M為BC邊上一動點,將線段OM繞點O按逆時針方向旋轉(zhuǎn)90°至ON,連接AN、CN,則△CAN周長的最小值為________.
AB,點M為BC邊上一動點,將線段OM繞點O按逆時針方向旋轉(zhuǎn)90°至ON,連接AN、CN,則△CAN周長的最小值為________.

查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】如圖,在△ABC中,∠BAC的平分線與BC的中垂線DE交于點E,過點E作AC邊的垂線,垂足為N,過點E作AB延長線的垂線,垂足為M.
(1)求證:BM=CN;
(2)若,AB=2,AC=8,求BM的長.

查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】看誰又快又準
(1)﹣0.5﹣(﹣3![]() )+2.75﹣(+7
)+2.75﹣(+7![]() )
)
(2)(﹣30)×(![]() )
)
(3)﹣12014﹣(2.5﹣2)×![]() [4﹣(﹣1)3]
[4﹣(﹣1)3]
(4)用簡便方法計算:99![]() ×(﹣9)
×(﹣9)
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】一名男生推鉛球,鉛球行進的高度y(單位:m)與水平距離x(單位:m)之間的關(guān)系是![]() .
.
(1)鉛球行進的最大高度是多少?
(2)該男生把鉛球推出的水平距離是多少?
(3)鉛球在下落的過程中,行進高度由![]() m變?yōu)?/span>
m變?yōu)?/span>![]() m時,鉛球行進的水平距離是多少?
m時,鉛球行進的水平距離是多少?
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com