【題目】公元前5世紀，畢達哥拉斯學派中的一名成員希伯索斯發現了無理數 
，導致了第一次數學危機， 是無理數的證明如下： 假設 是有理數，那么它可以表示成 
（p與q是互質的兩個正整數）．于是（ ）2=（ ）2=2，所以，q2=2p2 ． 于是q2是偶數，進而q是偶數，從而可設q=2m，所以（2m）2=2p2 ， p2=2m2 ， 于是可得p也是偶數．這與“p與q是互質的兩個正整數”矛盾．從而可知“ 是有理數”的假設不成立，所以， 是無理數．
這種證明“ 是無理數”的方法是（ ）
A.綜合法
B.反證法
C.舉反例法
D.數學歸納法
津橋教育計算小狀元系列答案科目：初中數學 來源： 題型：
【題目】如圖，AD是等腰△ABC底邊BC上的高．點O是AC中點，延長DO到E，使OE=OD，連接AE，CE．
（1）求證：四邊形ADCE的是矩形；
（2）若AB=17，BC=16，求四邊形ADCE的面積．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】已知多項式x3﹣3xy2﹣4的常數是a，次數是b．
（1）則a=_____，b=_____；并將這兩數在數軸上所對應的點A、B表示出來；
（2）數軸上在B點右邊有一點C到A、B兩點的距離之和為11，求點C在數軸上所對應的數；
（3）在數軸上是否存在點P，使P到A、B、C的距離和等于12？若存在，求點P對應的數；若不存在，請說明理由．
（4）在數軸上是否存在點P，使P到A、B、C的距離和最小？若存在，求該最小值，并求此時P點對應的數；若不存在，請說明理由．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】體育委員統計了全班同學60秒跳繩的次數，并列出下面的頻數分布表：
次數 | 60≤x＜90 | 90≤x＜120 | 120≤x＜150 | 150≤x＜180 | 180≤x＜210 |
頻數 | 16 | 25 | 9 | 7 | 3 |
（1）全班有多少同學？
（2）組距是多少？組數是多少？
（3）跳繩次數x在120≤x＜180范圍的同學有多少？占全班同學的百分之幾（精確到0.1%）？
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，已知線段AB=2，MN⊥AB于點M，且AM=BM，P是射線MN上一動點，E，D分別是PA，PB的中點，過點A，M，D的圓與BP的另一交點C（點C在線段BD上），連結AC，DE．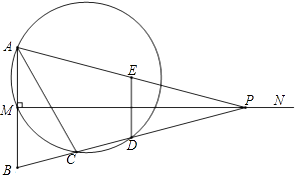
（1）當∠APB=28°時，求∠B和 
的度數；
（2）求證：AC=AB．
（3）在點P的運動過程中
①當MP=4時，取四邊形ACDE一邊的兩端點和線段MP上一點Q，若以這三點為頂點的三角形是直角三角形，且Q為銳角頂點，求所有滿足條件的MQ的值；
②記AP與圓的另一個交點為F，將點F繞點D旋轉90°得到點G，當點G恰好落在MN上時，連結AG，CG，DG，EG，直接寫出△ACG和△DEG的面積之比．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】一副三角板按如圖方式擺放，得到△ABD和△BCD，其中∠ADB=∠BCD=90°，∠A=60°，∠CBD=45°，E為AB的中點，過點E作EF⊥CD于點F．若AD=4cm，則EF的長為cm．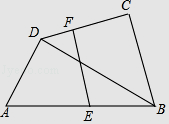 
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】從共享單車，共享汽車等共享出行到共享充電寶，共享雨傘等共享物品，各式各樣的共享經濟模式在各個領域迅速普及應用，越來越多的企業與個人成為參與者與受益者．根據國家信息中心發布的《中國分享經濟發展報告2017》顯示，2016年我國共享經濟市場交易額約為34520億元，比上年增長103%；超6億人參與共享經濟活動，比上年增加約1億人．
如圖是源于該報告中的中國共享經濟重點領域市場規模統計圖：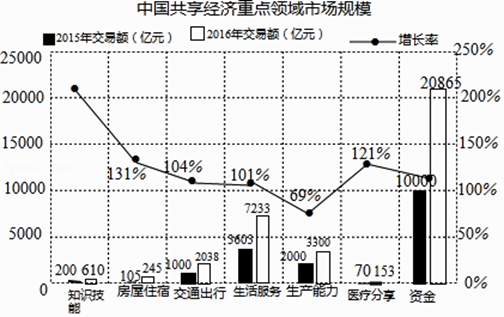
（1）請根據統計圖解答下列問題：
①圖中涉及的七個重點領域中，2016年交易額的中位數是億元．
②請分別計算圖中的“知識技能”和“資金”兩個重點領域從2015年到2016年交易額的增長率（精確到1%），并就這兩個重點領域中的一個分別從交易額和增長率兩個方面，談談你的認識．
（2）小宇和小強分別對共享經濟中的“共享出行”和“共享知識”最感興趣，他們上網查閱了相關資料，順便收集到四個共享經濟領域的圖標，并將其制成編號為A，B，C，D的四張卡片（除編號和內容外，其余完全相同）他們將這四張卡片背面朝上，洗勻放好，從中隨機抽取一張（不放回），再從中隨機抽取一張，請用列表或畫樹狀圖的方法求抽到的兩張卡片恰好是“共享出行”和“共享知識”的概率（這四張卡片分別用它們的編號A，B，C，D表示）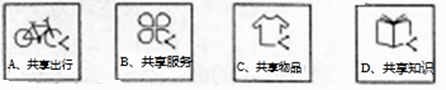
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】若關于x的不等式x﹣ 
＜1的解集為x＜1，則關于x的一元二次方程x2+ax+1=0根的情況是（ ）
A.有兩個相等的實數根
B.有兩個不相等的實數根
C.無實數根
D.無法確定
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
