
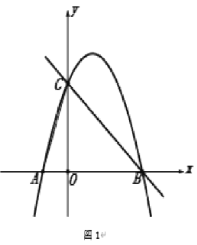
【題目】如圖,在平面直角坐標系中,點![]() 為坐標原點,拋物線
為坐標原點,拋物線![]() 交
交![]() 軸于
軸于![]() 、
、![]() 兩點,交
兩點,交![]() 軸于點
軸于點![]() ,
,![]() .
.
(1)求拋物線的解析式;
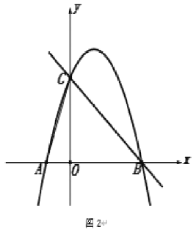
(2)如圖2,![]() 為第一象限內拋物線上一點,
為第一象限內拋物線上一點,![]() 的面積為3時,且
的面積為3時,且![]() ,求
,求![]() 點坐標;
點坐標;
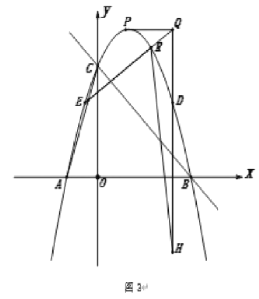
(3)如圖3,在(2)的條件下,![]() 、
、![]() 為拋物線上的點,且兩點關于拋物線對稱軸對稱,過
為拋物線上的點,且兩點關于拋物線對稱軸對稱,過![]() 作
作![]() 軸垂線交過點
軸垂線交過點![]() 且平行于
且平行于![]() 軸的直線于
軸的直線于![]() ,
,![]() 交拋物線于
交拋物線于![]() ,延長
,延長![]() 至
至![]() ,連接
,連接![]() ,
,![]() ,當線段
,當線段![]() 時,求點
時,求點![]() 的坐標.
的坐標.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]()
【解析】
(1)求出點C的坐標,利用待定系數法即可解決問題;
(2)如圖2中,作PH⊥AB于H,交BC于T.,作CE⊥PH于E,設P(![]() ,
,![]() ).構建方程即可解決問題;
).構建方程即可解決問題;
(3)如圖3中,作RM⊥DQ于M,連接EM.DH交AB于N.設D(n,![]() ).首先證明△EDQ∽△HDE,推出∠HEQ=90°,由∠REH+∠RMH=180°,推出E、H、M、R四點共圓,推出∠ERH=∠EMH,推出tan∠ERH=tan∠EMD=
).首先證明△EDQ∽△HDE,推出∠HEQ=90°,由∠REH+∠RMH=180°,推出E、H、M、R四點共圓,推出∠ERH=∠EMH,推出tan∠ERH=tan∠EMD=![]() ,推出DM=
,推出DM=![]() (n-1),推出QM=
(n-1),推出QM=![]() ,由RM∥DE,可得
,由RM∥DE,可得![]() ,推出RM=
,推出RM=![]() ,可得點R的坐標
,可得點R的坐標![]() ,把點R坐標代入
,把點R坐標代入![]() ,轉化為方程解決問題即可.
,轉化為方程解決問題即可.
(1)對于拋物線![]() ,
,
令y=0,得到![]() ,解得
,解得![]() 或3,
或3,
∴A(-1,0),B(3,0),
∴OB=3,
∵∠ABC=45°,
∴OC=OB=3,
∴C(0,3),把(0,3)代入![]() 得到
得到![]() ,
,
∴拋物線的解析式為![]() ;
;
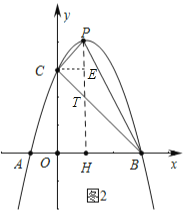
(2)如圖2中,作PH⊥AB于H,交BC于T,作CE⊥PH于E,設P(![]() ,
,![]() ).
).
∵B(3,0),C(0,3),
設直線BC的解析式為![]() ,
,
把B(3,0)代入得:![]() ,
,
解得:![]() ,
,
∴直線BC的解析式為![]() ,
,
∴T![]() ,
,
∵![]()
![]()
![]() ,
,
整理得:![]() ,
,
∴![]() 或2,
或2,
∵∠PCB>45°,
∴![]() ,
,
∴點P的坐標為(1,4);
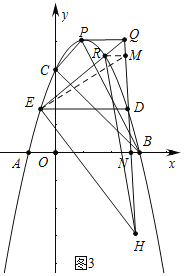
(3)如圖3中,作RM⊥DQ于M,連接EM,DH交AB于N.設D(n,![]() ).
).
∵D、E兩點關于拋物線對稱軸對稱,點P的坐標(1,4),拋物線對稱軸為![]() ,
,
∴PQ∥DE∥![]() 軸,DQ⊥
軸,DQ⊥![]() 軸,
軸,
∴Q(n,4),
∴DE=![]() ,DQ=
,DQ=![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,
,
∵∠EDQ=∠EDH=90°,
∴△EDQ∽△HDE,
∴∠DEQ=∠EHD,
∵∠DEQ+∠EQD=90°,
∴∠EHD+∠EQD=90°,
∴∠HEQ=90°,
∵∠REH+∠RMH=180°,
∴E、H、M、R四點共圓,
∴∠ERH=∠EMH,
∴tan∠ERH=tan∠EMD=![]() ,
,
∴DM=![]() ,
,
∴QM=DQ-DM=![]() ,
,
∵RM⊥DQ,
∴RM∥DE,
∴![]() ,即
,即 ,
,
∴RM=![]() ,
,
∴點R的坐標為![]() ,
,
即![]() ,
,
把點R坐標代入![]() 得到:
得到:
![]() ,
,
解得:![]() ,
,
∴點D的坐標為(![]() ,
,![]() ).
).


科目:初中數學 來源: 題型:
【題目】已知:△ABC 內接于⊙O,過點 A 作⊙O 的切線交 CB 的延長線于點 P,且∠PAB=45°.
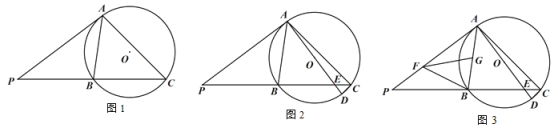
(1)如圖 1,求∠ACB 的度數;
(2)如圖 2,AD 是⊙O 的直徑,AD 交 BC 于點 E,連接 CD,求證:AC CD ![]() ;
;
(3)如圖 3 ,在(2)的條件下,當 BC 4![]() CD 時,點 F,G 分別在 AP,AB 上,連接 BF,FG,∠BFG=∠P,且 BF=FG,若 AE=15,求 FG 的長.
CD 時,點 F,G 分別在 AP,AB 上,連接 BF,FG,∠BFG=∠P,且 BF=FG,若 AE=15,求 FG 的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某農戶今年1月初以20000元/畝的價格承包了10畝地用來種植某農作物,已知若按傳統種植,每月每畝能產出3000千克,每畝的種植費用為2500元;若按科學種植,每月每畝產量可增加![]() ,但種植費用會增加2000元/畝,且前期需要再投入25萬元,花費4個月的時間進行生長環境的改善,改善期間無法種植.已知每千克農作物市場售價為3元,每月底一次性全部出售,假設前
,但種植費用會增加2000元/畝,且前期需要再投入25萬元,花費4個月的時間進行生長環境的改善,改善期間無法種植.已知每千克農作物市場售價為3元,每月底一次性全部出售,假設前![]() 個月銷售總額為
個月銷售總額為![]() (萬元).
(萬元).
(1)當![]() 時,分別求出兩種種植方法下的銷售總額
時,分別求出兩種種植方法下的銷售總額![]() ;
;
(2)問:若該農戶選擇科學種植,幾個月后能夠收回成本?
(3)在(2)的條件下,假如從2019年1月初算起,那么至少要到何時,該農戶獲得的總利潤能夠超過傳統種植同樣時間內所獲得的總利潤?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知拋物線![]() 的最低點為 D(0,2)
的最低點為 D(0,2)
(1)求 m, n 的值
(2)直線 y=kx+4 交 y 軸于點 F,與拋物線交于 A,B 兩點,直線 AD 交 x 軸于點 P.
①求證:BP//y 軸
②作 BQ⊥AD 交 y 軸于點 Q,求證:對于每個給定的實數 k,四邊形 FQPB 均為平行四邊形
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】綜合與實踐
在數學活動課上,老師給出![]() ,
,![]() ,
,![]() .點
.點![]() 為
為![]() 的中點,點
的中點,點![]() 在射線
在射線![]() 上運動,將線段
上運動,將線段![]() 繞點
繞點![]() 逆時針旋轉90°得到線段
逆時針旋轉90°得到線段![]() ,連接
,連接![]() ,
,![]() .過點
.過點![]() 作
作![]() ,交直線
,交直線![]() 于點
于點![]() .
.
(1)若點![]() 在線段
在線段![]() 上,如圖1,
上,如圖1,
①根據題意補全圖1(不要求尺規作圖);
②判斷![]() 與
與![]() 的數量關系并加以證明;
的數量關系并加以證明;
(2)若點![]() 為線段
為線段![]() 的延長線上一點,如圖2,且
的延長線上一點,如圖2,且![]() ,
,![]() ,補全圖2,求
,補全圖2,求![]() 的面積.
的面積.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】先閱讀,再解答問題.
恒等變形,是代數式求值的一個很重要的方法,利用恒等變形,可以把無理數運算轉化為有理數運算,可以把次數較高的代數式轉化為次數較低的代數式.如當x=![]() 時,求
時,求![]() ﹣x2﹣x+2的值,為解答這題,若直接把x=
﹣x2﹣x+2的值,為解答這題,若直接把x=![]() 代入所求的式中,進行計算,顯然很麻煩.我們可以通過恒等變形,對本題進行解答.
代入所求的式中,進行計算,顯然很麻煩.我們可以通過恒等變形,對本題進行解答.
方法一 將條件變形.因x=![]() ,得x﹣1=
,得x﹣1=![]() .再把所求的代數式變形為關于(x﹣1)的表達式.
.再把所求的代數式變形為關于(x﹣1)的表達式.
原式=![]() (x3﹣2x2﹣2x)+2
(x3﹣2x2﹣2x)+2
=![]() [x2(x﹣1)﹣x(x﹣1)﹣3x]+2
[x2(x﹣1)﹣x(x﹣1)﹣3x]+2
=![]() [x(x﹣1)2﹣3x]+2
[x(x﹣1)2﹣3x]+2
=![]() (3x﹣3x)+2
(3x﹣3x)+2
=2
方法二 先將條件化成整式,再把等式兩邊同時平方,把無理數運算轉化為有理數運算.由x﹣1=![]() ,可得x2﹣2x﹣2=0,即,x2﹣2x=2,x2=2x+2.
,可得x2﹣2x﹣2=0,即,x2﹣2x=2,x2=2x+2.
原式=![]() x(2x+2)﹣x2﹣x+2
x(2x+2)﹣x2﹣x+2
=x2+x﹣x2﹣x+2
=2
請參以上的解決問題的思路和方法,解決以下問題:
(1)若a2﹣3a+1=0,求2a3﹣5a2﹣3+![]() 的值;
的值;
(2)已知x=2+![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
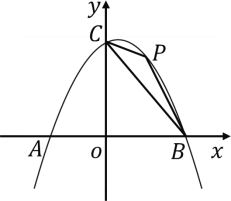
【題目】如圖,拋物線![]() 交
交![]() 軸于A(﹣3,0),B兩點,與y軸交于點C
軸于A(﹣3,0),B兩點,與y軸交于點C![]() ,連接AC,BC.點P是線段BC上方拋物線上的一個動點,點P的橫坐標為
,連接AC,BC.點P是線段BC上方拋物線上的一個動點,點P的橫坐標為![]() .
.
(1)求此拋物線的表達式;
(2)若點![]() ,求MA+MB的最小值,并求出此時點M的坐標.
,求MA+MB的最小值,并求出此時點M的坐標.
(3)求![]() 面積的最大值,并求出此時點P的坐標.
面積的最大值,并求出此時點P的坐標.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com