
【題目】平面內(nèi)的兩條直線有相交和平行兩種位置關系.




(1)如圖1,若![]() ,點
,點![]() 在
在![]() 外部,則有
外部,則有![]() ,又可證
,又可證![]() ,得
,得![]() ,將點
,將點![]() 移到
移到![]() 內(nèi)部,如圖2,以上結論是否成立?若成立,說明理由;若不成立,則
內(nèi)部,如圖2,以上結論是否成立?若成立,說明理由;若不成立,則![]() 之間有何數(shù)量關系?請證明你的結論;
之間有何數(shù)量關系?請證明你的結論;
(2)在如圖2中,將直線![]() 繞點
繞點![]() 逆時針方向旋轉一定角度交直線
逆時針方向旋轉一定角度交直線![]() 于點
于點![]() 如圖3,則
如圖3,則![]()
![]() 之間有何數(shù)量關系? (不需證明);
之間有何數(shù)量關系? (不需證明);
(3)根據(jù)(2)的結論,求如圖4中![]() 的度數(shù).
的度數(shù).
【答案】(1)不成立,![]() ;證明見解析;(2)
;證明見解析;(2)![]() ;(3)
;(3)![]() .
.
【解析】
(1)延長BP交CD于點E,根據(jù)AB∥CD得出∠B=∠BED,再由三角形外角的性質即可得出結論;
(2)連接QP并延長,由三角形外角的性質得出∠BPE=∠B+∠BQE,∠DPE=∠D+∠DQP,由此可得出結論;
(3)由(2)的結論得:∠AFG=∠B+∠E.∠AGF=∠C+∠D.再根據(jù)∠A+∠AFG+∠AGF=180°即可得出結論.
解:(1)不成立,結論是∠BPD=∠B+∠D.
延長BP交CD于點E,
∵AB∥CD,
∴∠B=∠BED,
又∵∠BPD=∠BED+∠D,
∴∠BPD=∠B+∠D;

(2)結論:∠BPD=∠BQD+∠B+∠D.
連接QP并延長,
∵∠BPE是△BPQ的外角,∠DPE是△PDQ的外角,
∴∠BPE=∠B+∠BQE,∠DPE=∠D+∠DQP,
∴∠BPE+∠DPE=∠B+∠D+∠BQE+∠DQP,
即∠BPD=∠BQD+∠B+∠D;

(3)由(2)的結論得:∠AFG=∠B+∠E.∠AGF=∠C+∠D.
又∵∠A+∠AFG+∠AGF=180°
∴∠A+∠B+∠C+∠D+∠E=180°.


 字詞句段篇系列答案
字詞句段篇系列答案科目:初中數(shù)學 來源: 題型:
【題目】已知E、F分別為正方形ABCD的邊BC、CD上的點,且∠EAF=45°.
(1)如圖①求證:BE+DF=EF;
(2)連接BD分別交AE、AF于M、N,
①如圖②,若AB=6![]() ,BM=3,求MN.
,BM=3,求MN.
②如圖③,若EF∥BD,求證:MN=CE.

查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】根據(jù)所學知識完成小題:
(1)如圖1,銳角△ABC中,分別以AB、AC為邊向外作等邊△ABE和等邊△ACD,連接BD,CE,試猜想BD與CE的大小關系,并說明理由.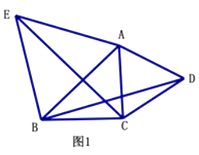
(2)【深入探究】如圖2,△ABC中,∠ABC=45°,AB=5cm,BC=3cm,分別以AB、AC為邊向外作正方形ABNE和正方形ACMD,連接BD,求BD的長.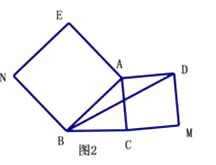
(3)如圖3,在(2)的條件下,以AC為直角邊在線段AC的左側作等腰直角△ACD,求BD的長.
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】如圖,O是正△ABC內(nèi)一點,OA=6,OB=8,OC=10,將線段BO以點B為旋轉中心逆時針旋轉60°得到線段BO′,下列結論:①△BO′A可以由△BOC繞點B逆時針旋轉60°得到;②點O與O′的距離為8;③S四邊形AOBO′=24+12![]() ;④S△AOC+S△AOB=24+9
;④S△AOC+S△AOB=24+9![]() ;⑤S△ABC=36+25
;⑤S△ABC=36+25![]() ; 其中正確的結論有( )
; 其中正確的結論有( )
A.1個
B.2個
C.3個
D.4個
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com