Question

【題目】如圖，面積為6的平行四邊形紙片ABCD中，AB=3，∠BAD=45°，按下列步驟進行裁剪和拼圖．
第一步：如圖①，將平行四邊形紙片沿對角線BD剪開，得到△ABD和△BCD紙片，再將△ABD紙片沿AE剪開（E為BD上任意一點），得到△ABE和△ADE紙片；
第二步：如圖②，將△ABE紙片平移至△DCF處，將△ADE紙片平移至△BCG處；
第三步：如圖③，將△DCF紙片翻轉過來使其背面朝上置于△PQM處（邊PQ與DC重合，△PQM和△DCF在DC同側），將△BCG紙片翻轉過來使其背面朝上置于△PRN處，（邊PR與BC重合，△PRN和△BCG在BC同側）．
則由紙片拼成的五邊形PMQRN中，對角線MN長度的最小值為 ．

Answer 1

【答案】
【解析】解：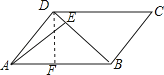

∵△ABE≌△CDF≌△PMQ，
∴AE=DF=PM，∠EAB=∠FDC=∠MPQ，
∵△ADE≌△BCG≌△PNR，
∴AE=BG=PN，∠DAE=∠CBG=∠RPN，
∴PM=PN，
∵四邊形ABCD是平行四邊形，
∴∠DAB=∠DCB=45°，
∴∠MPN=90°，
∴△MPN是等腰直角三角形，
當PM最小時，對角線MN最小，即AE取最小值，
∴當AE⊥BD時，AE取最小值，
過D作DF⊥AB于F，
∵平行四邊形ABCD的面積為6，AB=3，
∴DF=2，
∵∠DAB=45°，
∴AF=DF=2，
∴BF=1，
∴BD= = ，∴AE= = = ，∴MN= AE= ，
故答案為： ．
根據平移和翻折的性質得到△MPN是等腰直角三角形，于是得到當PM最小時，對角線MN最小，即AE取最小值，當AE⊥BD時，AE取最小值，過D作DF⊥AB于F，根據平行四邊形的面積得到DF=2，根據等腰直角三角形的性質得到AF=DF=2，由勾股定理得到BD= = ，根據三角形的面積得到AE= = = ，即可得到結論．本題考查了平移的性質，翻折的性質，勾股定理，平行四邊形的性質，正確的識別圖形是解題的關鍵．