
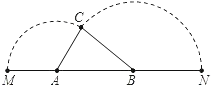
【題目】已知A、B是線段MN上的兩點,MN=4,MA=1,MB>1.以A為中心順時針旋轉點M,以B為中心逆時針旋轉點N,使M、N兩點重合成一點C,構成△ABC.設AB=x,請解答:(1)x的取值范圍______;
(2)若△ABC是直角三角形,則x的值是______.
【答案】1<x<2 x![]() 或x
或x![]() .
.
【解析】
(1)因為所求AB或x在△ABC中,所以可利用三角形三邊之間的關系即兩邊之和大于第三邊,兩邊之差小于第三邊進行解答.
(2)應該分情況討論,因為不知道在三角形中哪一個是作為斜邊存在的.所以有三種情況,即:①若AC為斜邊,則1=x2+(3-x)2,即x2-3x+4=0,無解;②若AB為斜邊,則x2=(3﹣x)2+1,解得x![]() ,滿足1<x<2;③若BC為斜邊,則(3﹣x)2=1+x2,解得:x
,滿足1<x<2;③若BC為斜邊,則(3﹣x)2=1+x2,解得:x![]() ,滿足1<x<2;
,滿足1<x<2;
解:
(1)∵MN=4,MA=1,AB=x,
∴BN=4﹣1﹣x=3﹣x,
由旋轉的性質得:MA=AC=1,BN=BC=3﹣x,
由三角形的三邊關系得
![]() ,
,
∴x的取值范圍是1<x<2.
故答案為:1<x<2;
(2)∵△ABC是直角三角形,
∴若AC為斜邊,則1=x2+(3﹣x)2,即x2﹣3x+4=0,無解,
若AB為斜邊,則x2=(3﹣x)2+1,解得:x![]() ,滿足1<x<2,
,滿足1<x<2,
若BC為斜邊,則(3﹣x)2=1+x2,解得:x![]() ,滿足1<x<2,
,滿足1<x<2,
故x的值為:x![]() 或x
或x![]() .
.
故答案為:x![]() 或x
或x![]() .
.


 名校課堂系列答案
名校課堂系列答案科目:初中數學 來源: 題型:
【題目】某校檢測學生跳繩水平,抽樣調查了部分學生的“1分鐘跳繩”成績,并制成了下面的頻數分布直方圖(每小組含最小值,不含最大值)和扇形圖

(1)D組的人數是 人,補全頻數分布直方圖,扇形圖中m= ;
(2)本次調查數據中的中位數落在 組;
(3)如果“1分鐘跳繩”成績大于或等于120次為優秀,那么該校4500名學生中“1分鐘跳繩”成績為優秀的大約有多少人?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】為弘揚中華傳統文化,黔南州近期舉辦了中小學生“國學經典大賽”.比賽項目為:A.唐詩;B.宋詞;C.論語;D.三字經.比賽形式分“單人組”和“雙人組”.
(1)小麗參加“單人組”,她從中隨機抽取一個比賽項目,恰好抽中“三字經”的概率是多少?
(2)小紅和小明組成一個小組參加“雙人組”比賽,比賽規則是:同一小組的兩名隊員的比賽項目不能相同,且每人只能隨機抽取一次,則恰好小紅抽中“唐詩”且小明抽中“宋詞”的概率是多少?請用畫樹狀圖或列表的方法進行說明.
查看答案和解析>>
科目:初中數學 來源: 題型:
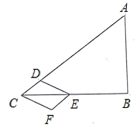
【題目】如圖,在![]() 中,
中,![]() ,
,![]() ,
,![]() .動點
.動點![]() 從點
從點![]() 出發,沿線段
出發,沿線段![]() 向終點
向終點![]() 以
以![]() /
/![]() 的速度運動,同時動點
的速度運動,同時動點![]() 從點
從點![]() 出發,沿折線
出發,沿折線![]() 以
以![]() /
/![]() 的速度向終點
的速度向終點![]() 運動,當有一點到達終點時,另一點也停止運動,以
運動,當有一點到達終點時,另一點也停止運動,以![]() 、
、![]() 為鄰邊作設
為鄰邊作設![]() 與
與![]() 重疊部分圖形的面積為
重疊部分圖形的面積為![]()
![]() 點
點![]() 運動的時間為
運動的時間為![]() .
.
(1)當點![]() 在
在![]() 邊上時,求
邊上時,求![]() 的長(用含
的長(用含![]() 的代數式表示);
的代數式表示);
(2)當點![]() 落在線段
落在線段![]() 上時,求
上時,求![]() 的值;
的值;
(3)求![]() 與
與![]() 之間的函數關系式
之間的函數關系式![]() ,并寫出自變量
,并寫出自變量![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖在Rt△ABC中,∠C=90°,BD平分∠ABC,過D作DE⊥BD交AB于點E,經過B,D,E三點作⊙O.
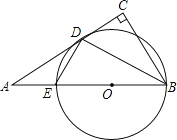
(1)求證:AC與⊙O相切于D點;
(2)若AD=15,AE=9,求⊙O的半徑.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某商場要經營一種新上市的文具,進價為20元,試營銷階段發現:當銷售單價是25元時,每天的銷售量為250件,銷售單價每上漲1元,每天的銷售量就減少10件
(1)寫出商場銷售這種文具,每天所得的銷售利潤![]() (元)與銷售單價
(元)與銷售單價![]() (元)之間的函數關系式;
(元)之間的函數關系式;
(2)求銷售單價為多少元時,該文具每天的銷售利潤最大;
(3)商場的營銷部結合上述情況,提出了A、B兩種營銷方案
方案A:該文具的銷售單價高于進價且不超過30元;
方案B:每天銷售量不少于10件,且每件文具的利潤至少為25元
請比較哪種方案的最大利潤更高,并說明理由
查看答案和解析>>
科目:初中數學 來源: 題型:
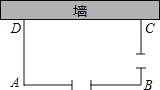
【題目】如圖,利用一面長為34米的墻,用鐵柵欄圍成一個矩形自行車場地ABCD,在AB和BC邊各有一個2米寬的小門(不用鐵柵欄)設矩形ABCD的邊AD長為x米,AB長為y米,矩形的面積為S平方米,且x<y.
(1)若所用鐵柵欄的長為40米,寫出y與x的函數關系式,并求出自變量x的取值范圍:
(2)在(1)的條件下,求S與x的函數關系式,并求出怎樣圍才能使矩形場地的面積為192平方米?
(3)在(2)的條件下,請直接寫出當矩形場地的面積大于192平方米時x的取值范圍.
查看答案和解析>>
科目:初中數學 來源: 題型:
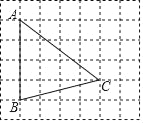
【題目】如圖,在每個小正方形的邊長為1的網格中,點A,B,C均在格點上.
(Ⅰ)AC的長等于_____;
(Ⅱ)在線段AC上有一點D,滿足AB2=ADAC,請在如圖所示的網格中,用無刻度的直尺,畫出點D,并簡要說明點D的位置是如何找到的(不要求證明)_____.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知關于x的方程![]() .
.
(1)求證:無論k取什么實數值,這個方程總有實數根;
(2)當![]() =3時,△ABC的每條邊長恰好都是方程
=3時,△ABC的每條邊長恰好都是方程![]() 的根,求△ABC的周長.
的根,求△ABC的周長.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com